Question

一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:

买饭时间（分）	1	2	3	4	5
频率	0.1	0.4	0.3	0.1	0.1

从第一个学生开始买饭时计时.

（Ⅰ）估计第三个学生恰好等待4分钟开始买饭的概率;

（Ⅱ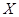）表示至第2分钟末已买完饭的人数,求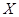的分布列及数学期望

 

Answer 1

【答案】

（Ⅰ）第2分钟末没有人买晚饭的概率；（Ⅱ）第三个学生恰好等待4分钟开始买饭的概率．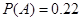

【解析】

试题分析：（Ⅰ）估计第三个学生恰好等待4分钟开始买饭的概率，包括①第一个学生买饭所需的时间为1分钟,且第二个学生买饭所需的时间为3分钟;②第一个学生买饭所需的时间为3分钟,且第二个学生买饭所需的时间为1分钟;③第一个和第二个学生买饭所需的时间均为2分钟.这三个事件，根据互斥事件的概率求法，即可求出概率;（Ⅱ）表示至第2分钟末已买完饭的人数,包括三种情况, 第2分钟末没有人买晚饭,第2分钟末有一人买饭,它包括:第一个学生买饭所需的时间为1分钟且第二个学生买饭所需的时间超过1分钟,或第一个学生买饭所需的时间为2分钟,第2分钟末,有两人买饭,故所有可能的取值为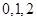,分别求出概率,从而写出的分布列,求出数学期望.

试题解析：（Ⅰ）设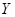表示学生买饭所需的时间,用频率估计概率,得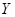的分布列如下:

	1	2	3	4	5
	0.1	0.4	0.3	0.1	0.1

(1)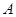表示事件“第三个学生恰好等待4分钟开始买饭”,则事件A对应三种情形:

①第一个学生买饭所需的时间为1分钟,且第二个学生买饭所需的时间为3分钟;②第一个学生买饭所需的时间为3分钟,且第二个学生买饭所需的时间为1分钟;③第一个和第二个学生买饭所需的时间均为2分钟.

所以 

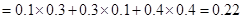        (6分)

（Ⅱ）所有可能的取值为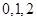 

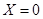对应第一个学生买饭所需的时间超过2分钟,

所以 

对应第一个学生买饭所需的时间为1分钟且第二个学生买饭所需的时间超过1分钟,或第一个学生买饭所需的时间为2分钟.

所以 

 

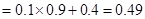
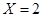对应两个学生买饭所需时间均为1分钟,

所以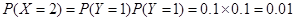 

所以的分布列为

	0	1	2
	0.5	0.49	0.01

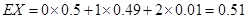           (12分)

考点：互斥事件的概率,分布列及数学期望.