
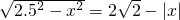 的不同实数根的个数是________.
的不同实数根的个数是________. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a |
| a |
| a |
| A、①③ | B、②④ | C、②③ | D、①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:江苏省东台市富安镇中学2008-2009学年度第二学期第一次月考高二数学试卷(文科) 题型:022
下面给出了关于复数的四种类比推理:
①复数的加减法运算可以类比多项式的加减法运算法则;
②由向量![]() 的性质
的性质![]() 类比得到复数z的性质|z|2=z2;
类比得到复数z的性质|z|2=z2;
③方程ax2+bx+c=0(a,b,c∈R)有两个不同实数根的条件是b2-4ac>0可以类比得到:方程az2+bz+c=0(a,b,c∈C)有两个不同复数根的条件是b2-4ac>0;
④由向量加法的几何意义可以类比得到复数加法的几何意义.
其中类比错误的是________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com