
设抛物线y2=2px(p>0)的焦点为F,直线l过点F交抛物线于A、B两点,点M在抛物线的准线上,O为坐标原点,设A(x1,y1),B(x2,y2).
(1)求证:y1y2=-p2;
(2)求证:直线MA、MF、MB的斜率成等差数列.
证明:
(1)设MA、MF、MB的斜率分别为k1、k、k2,A(x1,y1),?B(x2,y2),M(- 直线l的方程为:x=ty+![]() ,由
,由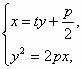 得y2-2pty-p2=0,故y1y2=-p2.
得y2-2pty-p2=0,故y1y2=-p2.
(2)由已知得y12=2px1,y22=2px2,
∴x1+![]() (y12+p2),x2+
(y12+p2),x2+![]() (y22+p2)=(y12+p2),k1+k2=
(y22+p2)=(y12+p2),k1+k2=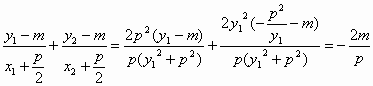 .
.
∵k=![]() ,∴k1+k2=2k.因此直线MA、MF、MB的斜率成等差数列.
,∴k1+k2=2k.因此直线MA、MF、MB的斜率成等差数列.
思路解析:本题第一问涉及直线与抛物线的交点,注意联立其方程消去一个未知数,利用根与系数间的关系从而达到目的;第二问在解决过程中注意充分利用点A、B在抛物线上这个已知条件.


科目:高中数学 来源:全优设计选修数学-2-2苏教版 苏教版 题型:047
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,点C在抛物线的准线上,且BC∥x轴,证明直线AC经过原点O.
查看答案和解析>>
科目:高中数学 来源:浙江省杭州学军中学2009届高三第十次月考数学(文)试题 题型:044
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A(x1,y1)、B(x2,y2)(y1>0,y2<0)两点,M是抛物线的准线上的一点,O是坐标原点,若直线MA、MF、MB的斜率分别记为:kMA=a、kMF=b、kMB=c,(如图)

(1)若y1y2=-4,求抛物线的方程;
(2)当b=2时,求证:a+c为定值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年云南省高二下学期期末考试理科数学卷 题型:填空题
设抛物线y2=2Px(P>0)的焦点为F,点A(0,2).若线段FA的中点B在抛物线上,则B到该抛物线准线的距离为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com