练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

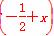    已知函数f(x)＝ax2＋bx＋c(a≠0)满足f(0)＝0，对于任意x∈R都有f(x)≥x，且f＝f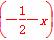，求函数f(x)的表达式．


    解析：因为f(0)＝0，所以c＝0.

    因为对于任意x∈R都有f＝f，

    所以函数f(x)的对称轴为x＝－，

    即－＝－，得a＝b.

    对于任意x∈R都有f(x)≥x，

    即ax2＋(b－1)x≥0对于任意x∈R都成立，

    所以a＞0，且Δ＝(b－1)2≤0.

    因为(b－1)2≥0, 所以b＝1，从而a＝1.

    所以f(x)＝x2＋x.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f(x)＝f′cos x＋sin x，则f的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有一个长度为5 m的梯子贴靠在笔直的墙上，假设其下端沿地板以3 m/s的速度离开墙脚滑动，当其下端离开墙脚1.4 m 时，梯子上端下滑的速度为____________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    经调查测算，某产品的年销售量(即该厂的年产量)x万件与年促销费用m万元(m≥0)满足x＝3－ (k为常数)，如果不搞促销活动，则该产品的年销售量只能是1万件．已知2012年生产该产品的固定投入为8万元，每生产1万件该产品需要再投入16万元，厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)．

    (1)将2012年该产品的利润y万元表示为年促销费用m万元的函数；

    (2)该厂家2012年的促销费用投入多少万元时，厂家的利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b，c∈R，函数f(x)＝ax2＋bx＋c.若f(0)＝f(4)＞f(1)，则(　　)

    A．a＞0,4a＋b＝0       B．a＜0,4a＋b＝0

    C．a＞0,2a＋b＝0       D．a＜0,2a＋b＝0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数F(x)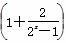＝·f(x)(x≠0)是偶函数，且f(x)不恒等于零，则 f(x)(　　)

    A．是奇函数

    B．可能是奇函数，也可能是偶函数

    C．是偶函数

    D．不是奇函数，也不是偶函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝a·2x＋b·3x，其中常数a，b满足ab≠0.

    (1)若ab>0，判断函数f(x)的单调性；

    (2)若ab<0，求f(x＋1)>f(x)时x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    扇形AOB的半径为1，圆心角为90°.点C，D，E将弧AB等分成四份．连接OC，OD，OE，从图中所有的扇形中随机取出一个，面积恰为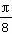的概率是(　　)

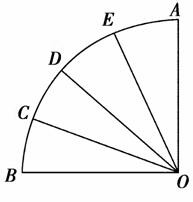
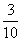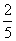    A.         B.         C.        D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    从一批苹果中，随机抽取50个，其重量(单位：克)的频数分布表如下：

    分组(重量)

    [80,85)

    [85,90)

    [90,95)

    [95,100)

    频数(个)

    5

    10

    20

    15

    (1)根据频数分布表计算苹果的重量在[90,95)的频率；

    (2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个，其中重量在[80,85)的有几个？

    (3)在(2)中抽出的4个苹果中，任取2个，求重量在[80,85)和[95,100)中各有1个的概率．

    查看答案和解析>>

    同步练习册答案