Question

讨论函数f(x)＝()的单调性，并求其值域．

Answer 1

答案：
解析：

　　解：函数的定义域为(－∞，＋∞)，设x₁、x₂∈(－∞，＋∞)，且x₁＜x₂．

　　则f(x₁)＝()＞0，f(x₂)＝()＞0，

　　．

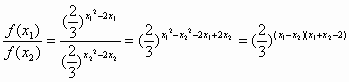　　当x₁＜x₂≤1时，x₁＋x₂＜2，即有x₁＋x₂－2＜0．

　　又因为x₁－x₂＜0，

　　所以(x₁－x₂)(x₁＋x₂－2)＞0，则0＜()＜1，

　　又对于任意的实数x，f(x)＞0，

　　所以f(x₁)＜f(x₂)．

　　所以函数f(x)＝()在(－∞，1]上是增函数．

　　当1≤x₁＜x₂时，x₁＋x₂＞2，即有x₁＋x₂－2＞0，

　　又因为x₁－x₂＜0，

　　所以(x₁－x₂)(x₁＋x₂－2)＜0，则()＞1．

　　又对于任意的实数x，f(x)＞0，

　　所以f(x₁)＞f(x₂)．

　　所以函数f(x)＝()在[1，＋∞)上是减函数．

　　综上，可知函数f(x)＝()在(－∞，1]上是增函数，在[1，＋∞)上是减函数．

　　因为x²－2x＝(x－1)²－1≥－1，0＜＜1，

　　所以0＜()≤()^－1＝，即函数的值域为(0，]．

　　思路分析：对于任意的实数x，()＞0恒成立，则在讨论函数的单调性时，可用作商法比较大小．求函数的值域可利用指数函数的单调性．