
设函数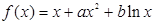 ,曲线
,曲线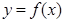 过点
过点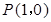 ,且在点
,且在点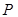 处的切线斜率为2.
处的切线斜率为2.
(Ⅰ)求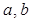 的值;
的值;
(Ⅱ)求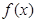 的极值点;
的极值点;
(Ⅲ)对定义域内任意一个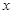 ,不等式
,不等式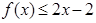 是否恒成立,若成立,请证明;若不成立,请说明理由。
是否恒成立,若成立,请证明;若不成立,请说明理由。
(Ⅰ)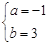 ;(Ⅱ)
;(Ⅱ)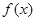 只有极大值点,且极大值点为
只有极大值点,且极大值点为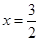 ;(Ⅲ)见解析。
;(Ⅲ)见解析。
【解析】
试题分析:(Ⅰ)∵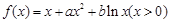
∴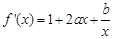 ...................1分
...................1分
∵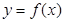 在点
在点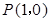 处的切线斜率为2
处的切线斜率为2
∴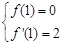 即
即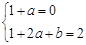 ......................2分
......................2分
故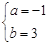 ..............................3分
..............................3分
(Ⅱ)∵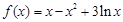 (
(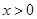 )
)
得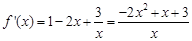 ................4分
................4分
即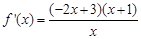
由 可得,
可得,
当 时,
时,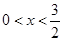 ...................5分
...................5分
当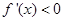 时,
时,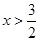 ............................6分
............................6分
列表可得:
|
|
|
|
|
|
|
+ |
0 |
— |
|
|
↗ |
|
↙ |
故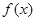 只有极大值点,且极大值点为
只有极大值点,且极大值点为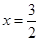 ..........................8分
..........................8分
(Ⅲ)令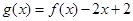 ,得
,得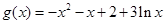 (
(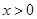 )............9分
)............9分
∴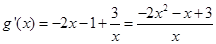
即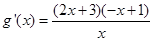 ..................10分
..................10分
由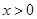 可得,
可得,
当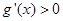 时,
时,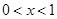
当 时,
时,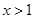 .........................11分
.........................11分
列表可得:
|
|
|
|
|
|
|
+ |
0 |
— |
|
|
↗ |
0 |
↙ |
由表可知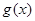 的最大值为
的最大值为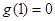
即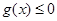 恒成立
恒成立
故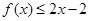 恒成立.......................12分
恒成立.......................12分
考点:导数的几何意义;利用导数研究函数的单调性;利用导数研究函数的极值;利用导数研究函数的最值。
点评:极值点的导数为零,但导数为零的点不一定是极值点。因此在求极值点的时候仅仅由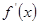 =0得到的点不一定是极值点,而应该加以验证。
=0得到的点不一定是极值点,而应该加以验证。


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:高中数学 来源: 题型:
 [选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.
[选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.
|
| π |
| 4 |
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林长春实验中学高三上学期第一次月考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
设函数 ,曲线
,曲线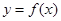 过点
过点 ,且在
,且在 点处的切线斜率为2.
点处的切线斜率为2.
(1)求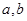 的值;
的值;
(2)证明: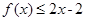
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二第七学段考试理科数学试卷(解析版) 题型:解答题
(本小题14分)设函数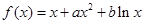 ,曲线
,曲线 过P(1,0),且在P点处的切斜线率为2.
过P(1,0),且在P点处的切斜线率为2.
(I)求a,b的值;
(II)证明: .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省高三百题集理科数学试卷(解析版)(三) 题型:解答题
设函数 ,曲线
,曲线 过P(1,0),且在P点处的切斜线率为2.
过P(1,0),且在P点处的切斜线率为2.
(I)求a,b的值;
(II)证明: 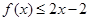
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com