
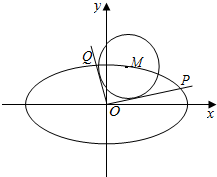
 如图,已知M(x0,y0)是椭圆C:$\frac{x^2}{6}+\frac{y^2}{3}=1$上的任一点,从原点O向圆M:${({x-{x_0}})^2}+{({y-{y_0}})^2}=2$作两条切线,分别交椭圆于点P、Q.
如图,已知M(x0,y0)是椭圆C:$\frac{x^2}{6}+\frac{y^2}{3}=1$上的任一点,从原点O向圆M:${({x-{x_0}})^2}+{({y-{y_0}})^2}=2$作两条切线,分别交椭圆于点P、Q.分析 (1)由题意得 $\frac{{|{k_1}{x_0}-{y_0}|}}{{\sqrt{1+k_1^2}}}=\sqrt{2}$,从而化简可得$(x_0^2-2)k_1^2-2{x_0}{y_0}{k_1}+y_0^2-2=0$,同理可得$(x_0^2-2)k_2^2-2{x_0}{y_0}{k_2}+y_0^2-2=0$;从而可知k1,k2是方程$(x_0^2-2)k_{\;}^2-2{x_0}{y_0}k+y_0^2-2=0$的两个不相等的实数根,从而可得${k_1}•{k_2}=\frac{y_0^2-2}{x_0^2-2}$,再由$y_0^2=3-\frac{1}{2}x_0^2$证明即可;
(2)可判断B是定值,定值为9,证明方法有两种:(法一):按斜率是否存在分类讨论,(i)当直线OP、OQ不落在坐标轴上时,设P(x1,y1),Q(x2,y2),从而联立方程可得${x_1}^2+{y_1}^2=\frac{{6(1+{k_1}^2)}}{{1+2{k_1}^2}}$,${x_2}^2+{y_2}^2=\frac{{6(1+{k_2}^2)}}{{1+2{k_2}^2}}$,从而化简$O{P^2}+O{Q^2}={x_1}^2+{y_1}^2+{x_2}^2+{y_2}^2$=$\frac{{6(1+{k_1}^2)}}{{1+2{k_1}^2}}+\frac{{6(1+{k_2}^2)}}{{1+2{k_2}^2}}$=$\frac{{9+18{k_1}^2}}{{1+2{k_1}^2}}$=9;(ii)当直线OP、OQ落在坐标轴上时,显然有B=9.(法二):按斜率是否存在分类讨论,(i)当直线OP、OQ不落在坐标轴上时,设P(x1,y1),Q(x2,y2),由${k_1}{k_2}=-\frac{1}{2}$可得$y_1^2y_2^2=\frac{1}{4}x_1^2x_2^2$,再由方程化简可得$x_1^2+x_2^2=6$,从而解得.
解答 解:(1)证明:∵直线OP:y=k1x以及OQ:y=k2x与圆M相切,
∴$\frac{{|{k_1}{x_0}-{y_0}|}}{{\sqrt{1+k_1^2}}}=\sqrt{2}$,
化简得:$(x_0^2-2)k_1^2-2{x_0}{y_0}{k_1}+y_0^2-2=0$
同理:$(x_0^2-2)k_2^2-2{x_0}{y_0}{k_2}+y_0^2-2=0$,
∴k1,k2是方程$(x_0^2-2)k_{\;}^2-2{x_0}{y_0}k+y_0^2-2=0$的两个不相等的实数根,
∴${k_1}•{k_2}=\frac{y_0^2-2}{x_0^2-2}$,
∵点M(x0,y0)在椭圆C上,
∴$\frac{{{x_0}^2}}{6}+\frac{{{y_0}^2}}{3}=1$,即$y_0^2=3-\frac{1}{2}x_0^2$,
∴${k_1}{k_2}=\frac{{1-\frac{1}{2}x_0^2}}{x_0^2-2}=-\frac{1}{2}$,为定值.
(2)B是定值,定值为9,证明如下,
法一:(i)当直线OP、OQ不落在坐标轴上时,设P(x1,y1),Q(x2,y2),
联立$\left\{\begin{array}{l}y={k_1}x\\ \frac{x^2}{6}+\frac{y^2}{3}=1\end{array}\right.$解得$\left\{\begin{array}{l}{x_1}^2=\frac{6}{{1+2{k_1}^2}}\\{y_1}^2=\frac{{6{k_1}^2}}{{1+2{k_1}^2}}.\end{array}\right.$,
故${x_1}^2+{y_1}^2=\frac{{6(1+{k_1}^2)}}{{1+2{k_1}^2}}$,
同理得,${x_2}^2+{y_2}^2=\frac{{6(1+{k_2}^2)}}{{1+2{k_2}^2}}$,
∵${k_1}{k_2}=-\frac{1}{2}$,
∴$O{P^2}+O{Q^2}={x_1}^2+{y_1}^2+{x_2}^2+{y_2}^2$
=$\frac{{6(1+{k_1}^2)}}{{1+2{k_1}^2}}+\frac{{6(1+{k_2}^2)}}{{1+2{k_2}^2}}$
=$\frac{{6(1+{k_1}^2)}}{{1+2{k_1}^2}}+\frac{{6(1+{{(-\frac{1}{{2{k_1}}})}^2})}}{{1+2{{(-\frac{1}{{2{k_1}}})}^2}}}$
=$\frac{{9+18{k_1}^2}}{{1+2{k_1}^2}}$=9;
(ii)当直线OP、OQ落在坐标轴上时,显然有B=9;
综上所述,B=9.
法二:(i)当直线OP、OQ不落在坐标轴上时,设P(x1,y1),Q(x2,y2),
∵${k_1}{k_2}=-\frac{1}{2}$,
∴$y_1^2y_2^2=\frac{1}{4}x_1^2x_2^2$,
∵P(x1,y1),Q(x2,y2)在椭圆C上,
∴$\left\{\begin{array}{l}\frac{x_1^2}{6}+\frac{y_1^2}{3}=1\\ \frac{x_2^2}{6}+\frac{y_2^2}{3}=1\end{array}\right.$,即 $\left\{\begin{array}{l}y_1^2=3-\frac{1}{2}x_1^2\\ y_2^2=3-\frac{1}{2}x_2^2\end{array}\right.$,
∴$(3-\frac{1}{2}x_1^2)(3-\frac{1}{2}x_2^2)=\frac{1}{4}x_1^2x_2^2$,整理得$x_1^2+x_2^2=6$,
∴$y_1^2+y_2^2=({3-\frac{1}{2}x_1^2})+({3-\frac{1}{2}x_2^2})=3$,
∴B=9.
(ii)当直线OP、OQ落在坐标轴上时,显然有B=9,
综上所述,B=9.
点评 本题考查了椭圆与圆,直线的位置关系的应用及分类讨论的思想应用,同时考查了学生的化简运算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\sqrt{2},\sqrt{2})$ | B. | $(-∞,-\sqrt{2})∪(\sqrt{2},+∞)$ | C. | (-2,2) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C的中心在坐标原点,离心率为$\frac{1}{2}$,且它的短轴端点恰好是双曲线$\frac{y^2}{8}-\frac{x^2}{4}=1$的焦点.
已知椭圆C的中心在坐标原点,离心率为$\frac{1}{2}$,且它的短轴端点恰好是双曲线$\frac{y^2}{8}-\frac{x^2}{4}=1$的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
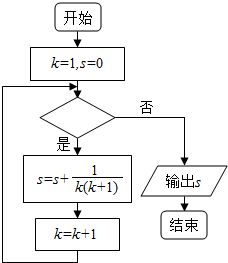
| A. | k≤2015 | B. | k≤2016 | C. | k≥2015 | D. | k≥2016 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com