
分析 (1)分别求出特征三角形是腰长为a 和底边长为2c,从而得到椭圆的相似比.
(2)设出椭圆Cb的方程,直线lMN的方程,根据两点关于直线对称的性质,求出直线lMN的方程,根据直线lMN与椭圆Cb有两个不同的交点,判别式大于零,求得实数b的取值范围.
解答 解:(1)椭圆C2与C1相似.-------------------(2分)
因为椭圆C2的特征三角形是腰长为4,底边长为4$\sqrt{3}$的等腰三角形,而椭圆C1的特征三角形是腰长为2,底边长为2$\sqrt{3}$的等腰三角形,因此两个等腰三角形相似,且相似比为2:1-------------------(4分)
(2)Cb:$\frac{x^2}{{4{b^2}}}+\frac{y^2}{b^2}$=1或$\frac{x^2}{b^2}+\frac{y^2}{{4{b^2}}}$=1
设lMN:y=-x+t,点M(x1,y1),N(x2,y2),MN中点为(x0,y0),
则$\left\{\begin{array}{l}{y=-x+t}\\{\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,所以5x2-8tx+4(t2-b2)=0-------------------(8分)
则x0=$\frac{4t}{5}$,y0=$\frac{t}{5}$------------------(9分)
因为中点在直线y=x+1上,所以有$\frac{t}{5}$=$\frac{4t}{5}$+1,t=-$\frac{5}{3}$-------------------(10分)
即直线lMN的方程为:y=-x-$\frac{5}{3}$,
由题意可知,直线lMN与椭圆Cb有两个不同的交点,
即方程5x2-8×(-$\frac{5}{3}$)x+4[(-$\frac{5}{3}$)2-b2]=0有两个不同的实数解,
所以$△=\frac{1600}{9}$-4×5×4×[(-$\frac{5}{3}$)2-b2]>0,即b>$\frac{{\sqrt{5}}}{3}$.
点评 本题考查直线和圆锥曲线的位置关系,两点关于直线对称的性质,求直线MN的方程是解决的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
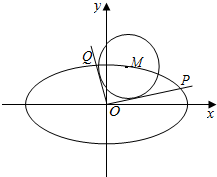 如图,已知M(x0,y0)是椭圆C:$\frac{x^2}{6}+\frac{y^2}{3}=1$上的任一点,从原点O向圆M:${({x-{x_0}})^2}+{({y-{y_0}})^2}=2$作两条切线,分别交椭圆于点P、Q.
如图,已知M(x0,y0)是椭圆C:$\frac{x^2}{6}+\frac{y^2}{3}=1$上的任一点,从原点O向圆M:${({x-{x_0}})^2}+{({y-{y_0}})^2}=2$作两条切线,分别交椭圆于点P、Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
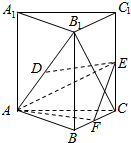 已知三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AB=AC,D,E,F分别为B1A,C1C,BC的中点.
已知三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AB=AC,D,E,F分别为B1A,C1C,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
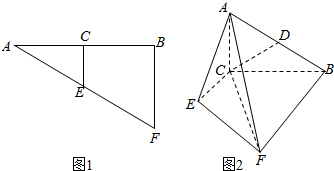
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±2x | B. | y=±$\frac{1}{2}x$ | C. | y=±4x | D. | y=±x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com