
分析 (1)分两类讨论,①当a=0时,f(x)为偶函数;②当a≠0时,f(x)既不是奇函数,也不是偶函数;
(2)先将函数表示为f(x)=$\left\{\begin{array}{l}{(x+\frac{1}{2})^2+\frac{7}{4}-a,x≥a}\\{(x-\frac{1}{2})^2+\frac{7}{4}+a,x<a}\end{array}\right.$,再结合二次函数的图象和性质,得出f(x)的单调区间,从而确定f(x)的最小值.
解答 解:(1)函数f(x)=x2+|x-a|+2的奇偶性,需要分下列两类讨论:
①当a=0时,函数f(-x)=(-x)2+|-x|+1=f(x),
所以,函数f(x)为偶函数;
②当a≠0时,f(a)=a2+1,f(-a)=a2+2|a|+1,f(a)≠f(-a)且f(a)≠-f(-a),
所以,函数f(x)既不是奇函数,也不是偶函数;
(2)f(x)=$\left\{\begin{array}{l}{(x+\frac{1}{2})^2+\frac{7}{4}-a,x≥a}\\{(x-\frac{1}{2})^2+\frac{7}{4}+a,x<a}\end{array}\right.$,函数的最小值需分三类讨论如下:
①当a>$\frac{1}{2}$时,结合二次函数的图象得出f(x)的单调区间为:
f(x)在(-∞,$\frac{1}{2}$)单调递减,在($\frac{1}{2}$,a)单调递增,(a,+∞)单调递增,
所以,仅当x=$\frac{1}{2}$时,函数取得最小值,f(x)min=f($\frac{1}{2}$)=$\frac{7}{4}$+a;
②当-$\frac{1}{2}$≤a≤$\frac{1}{2}$时,f(x)在(-∞,a)单调递减,在(a,+∞)单调递增,
所以,f(x)min=f(a)=a2+2;
③当a<-$\frac{1}{2}$时,结合二次函数的图象得出f(x)的单调区间为:
f(x)在(-∞,a)单调递减,在(a,-$\frac{1}{2}$)单调递减,(-$\frac{1}{2}$,+∞)单调递增,
所以,仅当x=-$\frac{1}{2}$时,函数取得最小值,f(x)min=f(-$\frac{1}{2}$)=$\frac{7}{4}$-a;
综合以上讨论得,函数f(x)的最小值f(x)min=$\left\{\begin{array}{l}{\frac{7}{4}+a,a>\frac{1}{2}}\\{a^2+2,-\frac{1}{2}≤a≤\frac{1}{2}}\\{\frac{7}{4}-a,a<-\frac{1}{2}}\end{array}\right.$.
点评 本题主要考查了函数奇偶性的判断和证明,并充分利用二次函数的图象和性质判断分段函数的单调区间和最值,体现了分类讨论与数形结合的解题思想,属于难题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
 如图,过曲线C:y=x3(x≥0)上点A1(2,8)作C的切线交x轴于点B1,过点B1作x轴的垂线交曲线C与点A2,过点A2作C的切线交x轴于点B2,再过点B2作x轴的垂线交曲线C与点A3,过点A3作C的切线交x轴于点B3,…、以此类推,得到一系列点:A1,B1,A2,B2,A3,B3,…记点An的横坐标为an.
如图,过曲线C:y=x3(x≥0)上点A1(2,8)作C的切线交x轴于点B1,过点B1作x轴的垂线交曲线C与点A2,过点A2作C的切线交x轴于点B2,再过点B2作x轴的垂线交曲线C与点A3,过点A3作C的切线交x轴于点B3,…、以此类推,得到一系列点:A1,B1,A2,B2,A3,B3,…记点An的横坐标为an.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
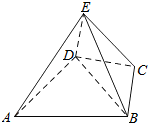 如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 5个 | C. | 6个 | D. | 7个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com