
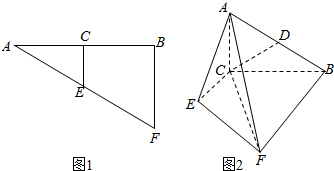
分析 (1)运用中位线定理和线面平行的判定定理,即可证得;
(2)由线面垂直的判定定理,面面垂直的判定定理即可证得.
解答 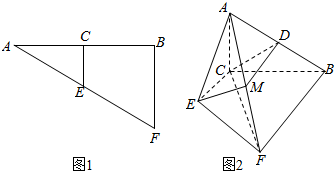 证明:(1)取AF中点M,连结DM,EM,
证明:(1)取AF中点M,连结DM,EM,
∵D,M分别是AB,AF的中点
∴DM是△ABF的中位线,
∴DM平行且等于$\frac{1}{2}$BF且CE平行且等于$\frac{1}{2}$BF,
四边形CDME是平行四边形,∴CD∥EM,
又EM?面AEF且CD?面AEF
∴CD∥面AEF;
(2)证明:由左图知CE⊥AC,CE⊥BC,
且右图中:AC∩BC=C,∴CE⊥面ABC,又CD?面ABC
∴CE⊥CD,∴四边形CDME为矩形,则EM⊥MD,
△AEF中EA=EF,M为AF的中点,
∴EM⊥AF,
∵AF∩MD=M,∴EM⊥面ABF,
又EM?面AEF,∴面AEF⊥面ABF.
点评 本题主要考查线面平行、垂直的判定和性质,以及面面垂直的判定和性质定理,考查学生分析解决问题的能力,属于中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 4 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
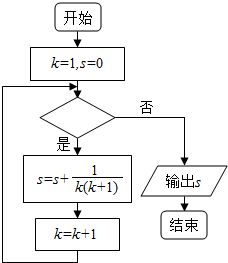
| A. | k≤2015 | B. | k≤2016 | C. | k≥2015 | D. | k≥2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
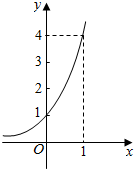 给出以下命题:
给出以下命题:| A. | (1)(2)(3) | B. | (1)(3)(5) | C. | (2)(4)(5) | D. | (1)(3)(4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com