
分析 由双曲线方程求出a、b、c,由双曲线的性质求出||PF1|-|PF2||=8,|F1F2|=10,由条件和余弦定理求出cos∠F1PF2的值,由平方关系求出sin∠F1PF2,根据三角形的面积公式求出△F1PF2的面积.
解答 解:由题意可得,a=4、b=3,则c=5,
则||PF1|-|PF2||=8,|F1F2|=10,
又|PF1|•|PF2|=36,则在△PF1F2中,
cos∠F1PF2=$\frac{|P{{F}_{1}|}^{2}+|P{{F}_{2}|}^{2}-|{F}_{1}{{F}_{2}|}^{2}}{2|P{F}_{1}||P{F}_{2}|}$
=$\frac{(|P{{F}_{1}|-|P{F}_{2}|)}^{2}+2|P{F}_{1}||P{F}_{2}|-|{F}_{1}{{F}_{2}|}^{2}}{2|P{F}_{1}||P{F}_{2}|}$
=$\frac{64+2×36-100}{2×36}$=$\frac{1}{2}$,
则sin∠F1PF2=$\sqrt{1-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
所以△F1PF2的面积S=$\frac{1}{2}$×|PF1|•|PF2|×sin∠F1PF2
=$\frac{1}{2}×36×\frac{\sqrt{3}}{2}$=9$\sqrt{3}$,
故答案为:9$\sqrt{3}$.
点评 本题考查双曲线的性质,余弦定理、同角三角函数关系式,以及三角形的面积公式等,属于中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
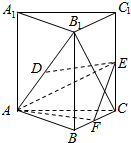 已知三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AB=AC,D,E,F分别为B1A,C1C,BC的中点.
已知三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AB=AC,D,E,F分别为B1A,C1C,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
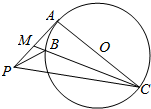 如右图所示,PA为圆O的切线,切点为A,AC是直径,M为PA的中点,MC与圆交于点B.
如右图所示,PA为圆O的切线,切点为A,AC是直径,M为PA的中点,MC与圆交于点B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.
如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com