
已知函数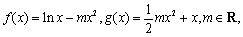 令
令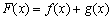 .
.
(Ⅰ)当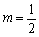 时,求函数
时,求函数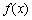 的单调递增区间;
的单调递增区间;
(Ⅱ)若关于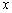 的不等式
的不等式 恒成立,求整数
恒成立,求整数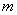 的最小值;
的最小值;
(Ⅲ)若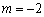 ,正实数
,正实数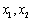 满足
满足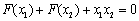 ,证明:
,证明: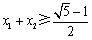 .
.
(Ⅰ)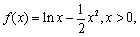
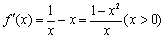
由 得
得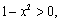 又
又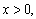 所以
所以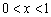 .所以
.所以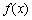 的单增区间为
的单增区间为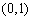 .
.
(Ⅱ)方法一:令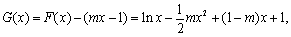
所以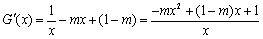 .
.
当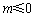 时,因为
时,因为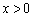 ,所以
,所以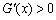 ,所以
,所以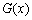 在
在 上是递增函数,
上是递增函数,
又因为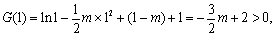 所以关于
所以关于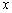 的不等式
的不等式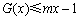 不能恒成立.
不能恒成立.
当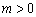 时,
时,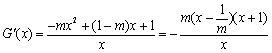 .
.
令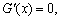 得
得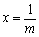 ,所以当
,所以当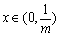 时,
时,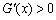 ;当
;当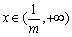 时,
时,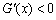 .
.
因此函数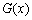 在
在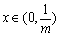 是增函数,在
是增函数,在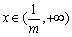 是减函数.
是减函数. 
故函数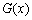 的最大值为
的最大值为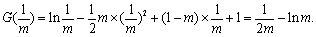 …………8分
…………8分
令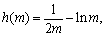 因为
因为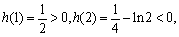
又因为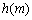 在
在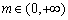 上是减函数,所以当
上是减函数,所以当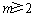 时,
时,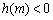 .
.
所以整数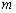 的最小值为. ……………10分
的最小值为. ……………10分
方法二:(2)由 恒成立,得
恒成立,得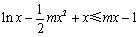 在
在 上恒成立.
上恒成立.
问题等价于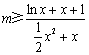 在
在 上恒成立.
上恒成立.
令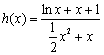 ,只要
,只要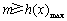 . ……………………6分
. ……………………6分
因为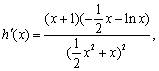 令
令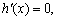 得
得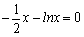 .
.
设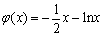 ,因为
,因为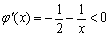 ,所以
,所以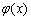 在
在 上单调递减,
上单调递减,
不妨设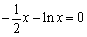 的根为
的根为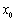 .当
.当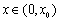 时,
时,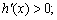 当
当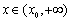 时,
时,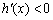 .
.
所以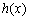 在
在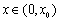 上是增函数;在
上是增函数;在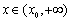 上是减函数.
上是减函数.
所以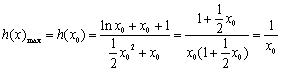 .
.
因为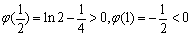

所以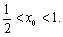 此时
此时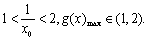 所以
所以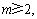 即整数
即整数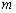 的最小值为2
的最小值为2
(Ⅲ)当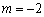 时,
时,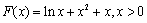
由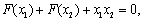 即
即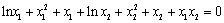
从而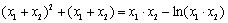
令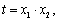 则由
则由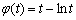 得,
得,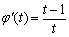
可知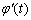 在区间(0,1)上单调递减,在区间
在区间(0,1)上单调递减,在区间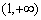 上单调递增。所以
上单调递增。所以
所以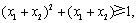 即
即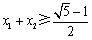 成立.
成立.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
将5名同学分到甲、乙、丙三个小组,若甲组至少两人,乙、丙两组每组至少一人,
则不同的分配方案种数
(A)80种 (B)120种 (C)140种 (D)50种
查看答案和解析>>
科目:高中数学 来源: 题型:
某餐厅的原料费支出 与销售额y(单位:万元)之间有如下数据,根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为
与销售额y(单位:万元)之间有如下数据,根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为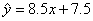 ,则表中的m的值为
,则表中的m的值为
|
| 2 | 4 | 5 | 6 | 8 |
|
| 25 | 35 |
| 55 | 75 |
A.50 B.55 C.60 D.65
查看答案和解析>>
科目:高中数学 来源: 题型:
若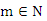 , 如题“m>0,则方程
, 如题“m>0,则方程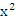
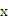
 有实根的逆否命题是
有实根的逆否命题是
若方程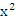
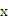
 有实根,则
有实根,则
若方程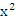
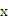
 有实根,则
有实根,则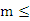
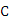 若方程
若方程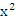
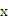
 没有实根,则
没有实根,则
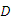 若方程
若方程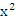
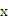
 没有实根,则
没有实根,则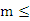
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com