练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．解不等式$\frac{2x-7}{{x}^{2}+x-6}$≥1．

    分析 通过讨论分母的符号，得到关于x的不等式组，解出即可．

    解答 解：原不等式可化为：
    $\left\{\begin{array}{l}{{x}^{2}+x-6＞0}\\{2x-7{≥x}^{2}+x-6}\end{array}\right.$无解，
    或$\left\{\begin{array}{l}{{x}^{2}+x-6＜0}\\{2x-7{≤x}^{2}+x-6}\end{array}\right.$，解得：-3＜x＜2，
    故不等式的解集是：{x|-3＜x＜2}．

    点评 本题考查了解不等式问题，考查分类讨论思想，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．已知集合A={x|（x+1）（x-2）≤0}，B={x|-2＜x＜2}，则A∩B=（　　）
    A．{x|-1≤x≤2}B．{x|-1≤x＜2}C．{x|-1＜x＜2}D．{x|-2＜x≤1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．在平面直角坐标系xoy中，己知圆C1：（x+3）2+（y-1）2=25和圆C2：（x-4）2+（y-2）2=4．
    （1）判断两圆的位置关系：
    （2）求过两圆的圆心的直线的方程：
    （3）若直线m过圆C1的圆心，且被圆C2截得的弦长为2$\sqrt{3}$，求直线m的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知三个球的表面积S1，S2，S3，满足$\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$=2$\sqrt{{S}_{3}}$，则它们的体积V1，V2，V3满足的等量关系是$\root{3}{{V}_{1}}$+$\root{3}{{V}_{2}}$=2$\root{3}{{V}_{3}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知等比数列{an}的各项均为正数，S2=7，S6=91，则S4=28．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．若（2-x）2013=a0+a1x+a2x2+…+a2013x2013，则$\frac{{a}_{0}+{a}_{2}+{a}_{4}+…{+a}_{2012}}{{a}_{1}+{a}_{3}+{a}_{5}+…+{a}_{2013}}$=（　　）
    A．$\frac{{3}^{2013}+1}{{3}^{2013}-1}$B．-$\frac{{3}^{2013}+1}{{3}^{2013}-1}$
    C．$\frac{{3}^{2012}+1}{{3}^{2012}-1}$D．-$\frac{{3}^{2012}+1}{{3}^{2012}-1}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知△ABC的面积为3，且满足2$\sqrt{3}$≤$\overrightarrow{AB}$•$\overrightarrow{AC}$≤6，设$\overrightarrow{AB}$、$\overrightarrow{AC}$的夹角为θ．
    （1）求θ的取值范围；
    （2）求函数f（θ）=2sin2（$\frac{π}{4}$+θ）-cos2θ的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

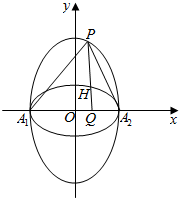    1．若两个椭圆的离心率相等，则称它们为“相似椭圆”．如图，在直角坐标系xOy中，已知椭圆C1：$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1，A1，A2分别为椭圆C1的左右顶点，椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”
    （1）求椭圆C2的方程；
    （2）设P为椭圆C2上异于A1，A2的任意一点，过P作PQ⊥x轴，垂足为Q，线段PQ交椭圆C1于H，求证：H为△PA1A2的垂心（垂心为三角形三条高的交点）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足：|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=1，|$\overrightarrow{a}$-2$\overrightarrow{b}$|≤2，则$\overrightarrow{b}$在$\overrightarrow{a}$上的投影长度的取值范围是（　　）
    A．[0，$\frac{1}{13}$]B．（0，$\frac{5}{13}$]C．[$\frac{1}{13}$，1]D．[$\frac{3}{4}$，1]

    查看答案和解析>>

    同步练习册答案