
| A. | [0,$\frac{1}{13}$] | B. | (0,$\frac{5}{13}$] | C. | [$\frac{1}{13}$,1] | D. | [$\frac{3}{4}$,1] |
分析 求出$\overrightarrow{a},\overrightarrow{b}$的夹角的范围,代入投影公式计算最值.
解答 解:∵|$\overrightarrow{a}$-2$\overrightarrow{b}$|≤2,∴${\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$≤4.即9+4-4$\overrightarrow{a}•\overrightarrow{b}$≤4.∴$\overrightarrow{a}•\overrightarrow{b}$≥$\frac{9}{4}$.
设$\overrightarrow{a},\overrightarrow{b}$的夹角为θ,则cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$≥$\frac{3}{4}$.又∵cosθ≤1,∴$\frac{3}{4}$≤cosθ≤1.
∴$\frac{3}{4}$≤|$\overrightarrow{b}$|cosθ≤1.
故选:D.
点评 本题考查了平面向量数量积的运算与应用,求出向量夹角是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
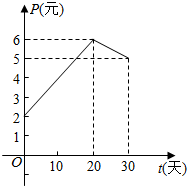 某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).
某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在底面为平行四边形的棱柱ABCD-A1B1C1D1中,AB=AD=2AA1=2,且∠A1AB=∠A1AD=∠BAD=60°,则四棱柱ABCD-A1B1C1D1的对角线AC1的长为( )
如图,在底面为平行四边形的棱柱ABCD-A1B1C1D1中,AB=AD=2AA1=2,且∠A1AB=∠A1AD=∠BAD=60°,则四棱柱ABCD-A1B1C1D1的对角线AC1的长为( )| A. | $\sqrt{14}$ | B. | 4 | C. | $\sqrt{17}$ | D. | $\sqrt{19}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com