Question

7．（1）求由曲线y=x²+2与y=3x，x=0，x=2所围成的平面图形的面积（画出图形）．
（2）已知a，b是正实数，求证：$\frac{a}{\sqrt{b}}+\frac{b}{\sqrt{a}}≥\sqrt{a}+\sqrt{b}$．

Answer 1

分析 （1）作出对应的图形，利用积分进行求解即可．
（2）由a，b是正实数，利用作差法得$（\frac{a}{\sqrt{b}}+\frac{b}{\sqrt{a}}）\;\;-\;\;（\sqrt{a}+\sqrt{b}）$=$\frac{{（\sqrt{a}-\sqrt{b}）}^{2}（\sqrt{a}+\sqrt{b}）}{\sqrt{ab}}$≥0，即可证得结论．

解答 解：（1）将y=3x代入y=x²+2得x²-3x+2=0，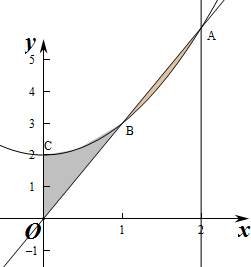
解得x=1或x=2，
即A（2，6），B（1，3），
则对应阴影部分的面积S=${∫}_{0}^{1}（{x}^{2}+2-3x）dx$+${∫}_{1}^{2}（3x-{x}^{2}-2）dx$=（$\frac{1}{3}$x³+2x-$\frac{3}{2}$x²）|${\;}_{0}^{1}$+（$\frac{3}{2}$x²-$\frac{1}{3}$x³+2x）|${\;}_{1}^{2}$
=$\frac{1}{3}$+2-$\frac{3}{2}$+$\frac{3}{2}$×2²-$\frac{1}{3}$×2³+2×2-（$\frac{3}{2}$-$\frac{1}{3}$+2）=5．
（2）证明：∵a，b是正实数，$（\frac{a}{\sqrt{b}}+\frac{b}{\sqrt{a}}）\;\;-\;\;（\sqrt{a}+\sqrt{b}）$=$\frac{a\sqrt{a}+b\sqrt{b}-a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}$ 
=$\frac{（\sqrt{a}-\sqrt{b}）（a-b）}{\sqrt{ab}}$=$\frac{{（\sqrt{a}-\sqrt{b}）}^{2}（\sqrt{a}+\sqrt{b}）}{\sqrt{ab}}$≥0，
∴$\frac{a}{\sqrt{b}}+\frac{b}{\sqrt{a}}≥\sqrt{a}+\sqrt{b}$成立．

点评 本题主要考查定积分在求面积的应用以及不等式的证明，要求熟练掌握常见函数的积分公式．