
 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当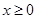 时有
时有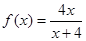 .
. 的解析式;②(选A题考生做)求
的解析式;②(选A题考生做)求 的值域;
的值域;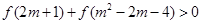 ,求
,求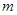 的取值范围.
的取值范围.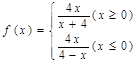 ;②
;②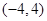 ;③
;③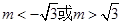
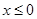 时,
时,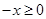 ,根据
,根据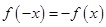 可推导出
可推导出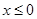 时
时 的解析式。注意最后将此函数写成分段函数的形式。②本题属用分离常数项法求函数值域。当
的解析式。注意最后将此函数写成分段函数的形式。②本题属用分离常数项法求函数值域。当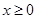 时将
时将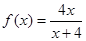 按分离常数项法将此函数化为
按分离常数项法将此函数化为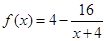 ,根据自变量的范围可推导出函数值的范围,因为此函数为奇函数所以值域也对称。故可得出
,根据自变量的范围可推导出函数值的范围,因为此函数为奇函数所以值域也对称。故可得出 的值域。③本题属用单调性“知二求一”解不等式问题。所以应先判断此函数的单调性。同②当
的值域。③本题属用单调性“知二求一”解不等式问题。所以应先判断此函数的单调性。同②当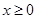 时将
时将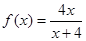 化为
化为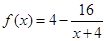 ,可知
,可知 在
在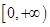 上是增函数,因为
上是增函数,因为 为奇函数,所以
为奇函数,所以 在上
在上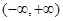 是增函数。根据单调性得两自变量的不等式,即可求得
是增函数。根据单调性得两自变量的不等式,即可求得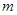 的取值范围。
的取值范围。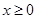 时有
时有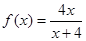 ∴当
∴当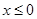 时,
时,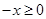 ∴
∴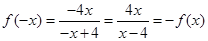 ∴
∴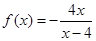 (
(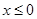 )∴
)∴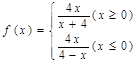 (6分)
(6分)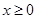 时有
时有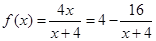 ∴
∴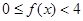 又∵
又∵ 是奇函数∴当
是奇函数∴当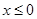 时
时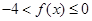 ∴
∴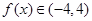 (A:13分)
(A:13分)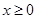 时有
时有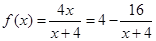 ∴
∴ 在
在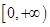 上是增函数,又∵
上是增函数,又∵ 是奇函数∴
是奇函数∴ 是在
是在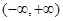 上是增函数,(B:13分)
上是增函数,(B:13分)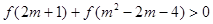 ∴
∴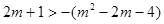 ∴
∴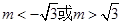


科目:高中数学 来源:不详 题型:单选题
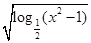 的定义域是 ( ).
的定义域是 ( ).A.[-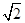 ,-1)∪(1, ,-1)∪(1,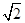 ] ] | B.(-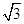 ,-1)∪(1, ,-1)∪(1,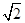 ) ) |
| C.[-2,-1)∪(1,2] | D.(-2,-1)∪(1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com