
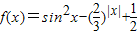 有下列四个个结论:
有下列四个个结论: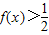 .
. .
.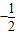 .
.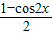 进行转化,然后利用cos2x和(
进行转化,然后利用cos2x和(  )|x|,求函数f(x)的最值,综合可得答案.
)|x|,求函数f(x)的最值,综合可得答案.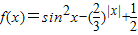 满足f(-x)=sin2x-
满足f(-x)=sin2x-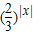 +
+ =f(x),故f(x)是偶函数,故①不正确.
=f(x),故f(x)是偶函数,故①不正确. )1000π>0,
)1000π>0, -(
-(  )1000π<
)1000π< ,因此结论②错.
,因此结论②错.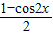 -(
-(  )|x|+
)|x|+ =1-
=1- cos2x-(
cos2x-(  )|x|,-1≤cos2x≤1,
)|x|,-1≤cos2x≤1, ≤1-
≤1- cos2x≤
cos2x≤ ,(
,(  )|x|>0.故1-
)|x|>0.故1- cos2x-(
cos2x-(  )|x|<
)|x|< ,即结论③错.
,即结论③错. )|x|在x=0时同时取得最大值,
)|x|在x=0时同时取得最大值, cos2x-(
cos2x-(  )|x|在x=0时可取得最小值-
)|x|在x=0时可取得最小值- ,即结论④是正确的.
,即结论④是正确的.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省连云港市赣榆县赣马高级中学高三数学小题狂做025(解析版) 题型:填空题
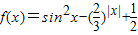 有下列四个个结论:
有下列四个个结论: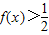 .
. .
. .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com