
【题目】根据下列条件,分别求抛物线的标准方程:
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,AF=5.
【答案】(1)y2=-12x.(2)y2=±2x或y2=±18x.
【解析】试题分析:(1)先将双曲线方程化为标准方程,根据方程可得左顶点,即得抛物线焦点,根据焦点坐标直接写出抛物线标准方程(2)根据焦点位置可设抛物线标准方程形式,设A点坐标,根据抛物线定义以及点在抛物线上列方程组解得p,即得抛物线方程
试题解析:解:(1)双曲线方程化为![]() -
-![]() =1,左顶点为(-3,0),由题意设抛物线方程为y2=-2px(p>0),且
=1,左顶点为(-3,0),由题意设抛物线方程为y2=-2px(p>0),且![]() =-3,∴p=6,∴方程为y2=-12x.
=-3,∴p=6,∴方程为y2=-12x.
(2)设所求焦点在x轴上的抛物线的方程为
y2=2px(p≠0),A(m,-3),
由抛物线定义,得5=AF=![]() .
.
又(-3)2=2pm,∴p=±1或p=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
点睛; 待定系数法求抛物线的标准方程
(1)根据抛物线焦点是在x轴上还是在y轴上,设出相应形式的标准方程,然后根据条件确定关于p的方程,解出p,从而写出抛物线的标准方程.
(2)当焦点位置不确定时,有两种方法解决.一种是分情况讨论,注意要对四种形式的标准方程进行讨论,对于焦点在x轴上的抛物线,为避免开口方向不确定可分为y2=2px(p>0)和y2=-2px(p>0)两种情况求解.另一种是设成y2=mx(m≠0),若m>0,开口向右;若m<0,开口向左;若m有两个解,则抛物线的标准方程有两个.同理,焦点在y轴上的抛物线可以设成x2=my(m≠0).如果不确定焦点所在的坐标轴,应考虑上述两种情况设方程.


科目:高中数学 来源: 题型:
【题目】8人排成一排照相,分别求下列条件下的不同照相方式的种数.
(1)其中甲、乙相邻,丙、丁相邻;
(2)其中甲、乙不相邻,丙、丁不相邻;
(要求写出解答过程,并用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点![]() ,
, ![]() 和一动点
和一动点![]() ,给出下列结论:
,给出下列结论:
①若![]() ,则点
,则点![]() 的轨迹是椭圆;
的轨迹是椭圆;
②若![]() ,则点
,则点![]() 的轨迹是双曲线;
的轨迹是双曲线;
③若![]() ,则点
,则点![]() 的轨迹是圆;
的轨迹是圆;
④若![]() ,则点
,则点![]() 的轨迹关于原点对称;
的轨迹关于原点对称;
⑤若直线![]() 与
与![]() 斜率之积等于
斜率之积等于![]() ,则点
,则点![]() 的轨迹是椭圆(除长轴两端点).
的轨迹是椭圆(除长轴两端点).
其中正确的是__________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假,并说明理由.
(1)x∈R,都有x2-x+1>![]() ;
;
(2)α,β,使cos(α-β)=cos α-cos β;
(3)x,y∈N,都有(x-y)∈N;
(4)x,y∈Z,使![]() x+y=3.
x+y=3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在实数集
在实数集![]() 上的图象是连续不断的,且对任意实数
上的图象是连续不断的,且对任意实数![]() 存在常数
存在常数![]() 使得
使得![]() 恒成立,则称
恒成立,则称![]() 是一个“关于
是一个“关于![]() 函数”.现有下列“关于
函数”.现有下列“关于![]() 函数”的结论:
函数”的结论:
①常数函数是“关于![]() 函数”;
函数”;
②正比例函数必是一个“关于![]() 函数”;
函数”;
③“关于![]() 函数”至少有一个零点;
函数”至少有一个零点;
④![]() 是一个“关于
是一个“关于![]() 函数”.
函数”.
其中正确结论的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系下,已知圆O:ρ=cosθ+sinθ和直线l:ρsin(θ﹣ ![]() )=
)= ![]() .
.
(1)求圆O和直线l的直角坐标方程;
(2)当θ∈(0,π)时,求直线l与圆O公共点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
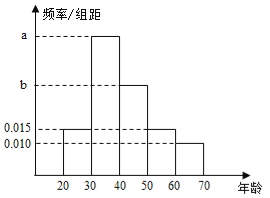
【题目】【广西南宁2017届高三检测】根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.
(1)已知![]() 、
、![]() ,
,![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() ,
,![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券,已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券,已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,2,3},集合B={x|a+1<x<6a﹣1},其中a∈R.
(1)写出集合A的所有真子集;
(2)若A∩B={3},求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com