
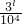 }={
}={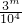 }={
}={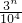 },其中{x}=x-[x],而[x]表示不超过x的最大整数.则这种三角形周长的最小值为________.
},其中{x}=x-[x],而[x]表示不超过x的最大整数.则这种三角形周长的最小值为________.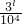 }={
}={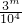 }={
}={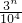 },可知3l、3m、3n的末四位数字相同即求满足3l°3m≡3n( mod 104)的l、m、n,利用取余以及数的分析,即可求得结论.
},可知3l、3m、3n的末四位数字相同即求满足3l°3m≡3n( mod 104)的l、m、n,利用取余以及数的分析,即可求得结论.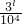 }={
}={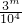 }={
}={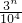 },∴3l、3m、3n的末四位数字相同,,
},∴3l、3m、3n的末四位数字相同,,

科目:高中数学 来源: 题型:
| 3l |
| 104 |
| 3m |
| 104 |
| 3n |
| 104 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 3l |
| 104 |
| 3m |
| 104 |
| 3n |
| 104 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省珠海一中高三(下)第一次调研数学试卷(理科)(解析版) 题型:填空题
 }={
}={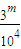 }={
}={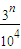 },其中{x}=x-[x],而[x]表示不超过x的最大整数.则这种三角形周长的最小值为 .
},其中{x}=x-[x],而[x]表示不超过x的最大整数.则这种三角形周长的最小值为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com