
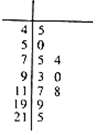
 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如图.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如图.分析 (1)从茎叶图中可发现该样本中空气质量优的天数为2,空气质量良的天数为4,从而求出该样本中空气质量优良的频率,由此能估计该月空气质量优良的天数.
(2)估计某天空气质量优良的概率为$\frac{3}{5}$,ξ的所有可能取值为0,1,2,3.且ξ~B(3,$\frac{3}{5}$),由此能求出结果.
解答 解:(1)从茎叶图中可发现该样本中空气质量优的天数为2,
空气质量良的天数为4,
故该样本中空气质量优良的频率为$\frac{6}{10}=\frac{3}{5}$,
从而估计该月空气质量优良的天数为$30×\frac{3}{5}=18$天.
(2)由(1)估计某天空气质量优良的概率为$\frac{3}{5}$,
ξ的所有可能取值为0,1,2,3.且ξ~B(3,$\frac{3}{5}$),
$P({ξ=0})={({\frac{2}{5}})^3}=\frac{8}{125},P({ξ=1})=C_3^1\frac{3}{5}{({\frac{2}{5}})^2}=\frac{36}{125},P({ξ=2})=C_3^2{({\frac{3}{5}})^2}\frac{2}{5}=\frac{54}{125}$,
$P({ξ=3})={({\frac{3}{5}})^3}=\frac{27}{125}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{8}{125}$ | $\frac{36}{125}$ | $\frac{54}{125}$ | $\frac{27}{125}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为M1,众数为M2,平均值为$\overline x$,则( )
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为M1,众数为M2,平均值为$\overline x$,则( )| A. | M1=M2=$\overline x$ | B. | M1=M2<$\overline x$ | C. | M1<M2<$\overline x$ | D. | M2<M1<$\overline x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$或$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (-2,-1] | C. | (-2,0] | D. | (-∞,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -$\frac{16}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ+$\frac{π}{8}$,kπ+$\frac{5}{8}$π](k∈Z) | B. | [-$\frac{3}{8}$π+kπ,$\frac{π}{8}$+kπ](k∈Z) | ||
| C. | [$\frac{π}{8}$+2kπ,$\frac{5π}{8}$+2kπ](k∈Z) | D. | [-$\frac{3}{8}$π+2kπ,$\frac{π}{8}$+2kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{2π}{5}$个单位长度 | B. | 向右平行移动$\frac{2π}{5}$个单位长度 | ||
| C. | 向左平行移动$\frac{4π}{5}$个单位长度 | D. | 向右平行移动$\frac{4π}{5}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com