练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    不等x|x|＜x的解集是（　　）
    A、{x|0＜x＜1}
    B、{x|-1＜x＜1}
    C、{x|0＜x＜1}或{x|x＜-1}，
    D、{x|-1＜x＜0，x＞1}
    考点：绝对值不等式
    专题：不等式的解法及应用
    分析：建议修改C为 {x|0＜x＜1，或 x＜-1}

    原不等式即x（|x|-1）＜0，等价转化为①
    x＞0
    |x|-1＜0
    ，或 ②
    x＜0
    |x|-1＞0
    ．分别求得①、②的解集，
    再取并集，即得所求．
    解答： 解：不等x|x|＜x，即 x（|x|-1）＜0，∴①
    x＞0
    |x|-1＜0
    ，或 ②
    x＜0
    |x|-1＞0
    ．
    解①可得 0＜x＜1，解②可得 x＜-1．
    把①②的解集取并集，即得原不等式的解集为 {x|0＜x＜1}或{x|x＜-1}，
    故选C．
    点评：本题主要考查绝对值不等式的解法，体现了分类讨论和等价转化的数学思想，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    极坐标方程p=cosθ化为直角坐标方程是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

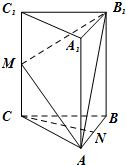    如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=BC=2，AB=2
    		2
    ，CC1=4，M是棱CC1上一点．
    （Ⅰ）求证：BC⊥AM；
    （Ⅱ）若M，N分别为CC1，AB的中点，求证：CN∥平面AB1M．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    记关于x的不等式
    x-a
    x-1
    ＜0的解集为P，不等式|x-1|＜1的解集为Q．
    （1）若a=3，求P；
    （2）若a=-1，求P∪Q．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在直角梯形ABCD中∠ABC=∠DAB=90°，∠CAB=30°，BC=1，AD=CD，把△DAC沿对角线AC折起后如图所示（点D记为点P），点P在平面ABC上的正投影E落在线段AB上，连接PB．若F是AC的中点，连接PF，EF．
    （1）求证：AC⊥平面PEF．
    （2）求直线PC与平面PAB所成的角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=xsinx-1在(-
    π
    2
    ，
    π
    2
    )    上的零点个数为（　　）
    A、5B、4C、3D、2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)=atanx+b
    3x
    +1    （a，b为实数），且f（lglog310）=5，则f（lglg3）=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    a
    =（-1，cosωx+
    		3
    sinωx），
    b
    =（f（x），cosωx），其中ω＞0，且
    a
    ⊥
    b
    ，又f（x）的图象两相邻对称轴的距离为
    3
    2
    π    ．
    （1）求ω的值；
    （2）求函数f（x）在[0，2π]上的单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    为了实现长沙经济区域一体化战略，湖南省政府计划对长沙市周边如图所示的A，B，C，D，E，F，G，H八个中小城市进行综合规划治理，第一期工程拟从这八个中小城市中选取3个城市，但要求没有任何两个城市相邻，则城市A被选中的概率为（　　）
    A、
    3
    8
    B、
    5
    28
    C、
    5
    13
    D、
    1
    2

    查看答案和解析>>

    同步练习册答案