
在下列命题中,所有正确命题的序号是 .
①三点确定一个平面;②两个不同的平面分别经过两条平行直线,则这两个平面互相平行;③过高的中点且平行于底面的平面截一棱锥,把棱锥分成上下两部分的体积之比为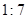 ;④平行圆锥轴的截面是一个等腰三角形.
;④平行圆锥轴的截面是一个等腰三角形.
科目:高中数学 来源: 题型:填空题
下列说法:
① “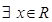 ,使
,使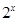 >3”的否定是“
>3”的否定是“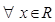 ,使
,使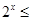 3”;
3”;
② 函数 的最小正周期是
的最小正周期是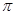 ;
;
③ “在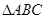 中,若
中,若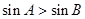 ,则
,则 ”的逆命题是真命题;
”的逆命题是真命题;
④ “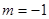 ”是“直线
”是“直线 和直线
和直线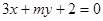 垂直”的充要条件;
垂直”的充要条件;
其中正确的说法是 (只填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列四个命题:
①若f(x+2)=f(2-x),则f(x)的图象关于x=2对称;
②若f(x+2)=f(2-x),则f(x)的图象关于y轴对称;
③函数y=f(2+x)与y=f(2-x)的图象关于x=2对称;
④函数y=f(2+x)与y=f(2—x)的图象关于y轴对称。正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知命题p:“?x∈[1,2], x2-a≥0”与命题q:“?x∈R,x2+2ax-8-6a=0”都是真命题,则a的取值范围为_________.
x2-a≥0”与命题q:“?x∈R,x2+2ax-8-6a=0”都是真命题,则a的取值范围为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知下列几个命题: ①已知F1、F2为两定点, =4,动点M满足
=4,动点M满足 ,则动点M的轨迹是椭圆。 ②一个焦点为
,则动点M的轨迹是椭圆。 ②一个焦点为 且与双曲线
且与双曲线 有相同的渐近线的双曲线标准方程是
有相同的渐近线的双曲线标准方程是 ③“若
③“若 =b,则a2=ab”的否命题。④若一个动圆的圆心在抛物线
=b,则a2=ab”的否命题。④若一个动圆的圆心在抛物线 上,且动圆恒与直线
上,且动圆恒与直线 相切,则动圆必过定点
相切,则动圆必过定点 。
。
其中真命题有____________
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出以下五个命题:①点 的一个对称中心
的一个对称中心
②设回时直线方程为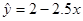 ,当变量x增加一个单位时,y大约减少2.5个单位
,当变量x增加一个单位时,y大约减少2.5个单位
③命题“在△ABC中,若 ,则△ABC为等腰三角形”的逆否命题为真命题
,则△ABC为等腰三角形”的逆否命题为真命题
④对于命题p:“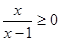 ”则
”则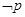 “
“ ”
”
⑤设 ,
,  ,则“
,则“ ”是 “
”是 “ ” 成立的充分不必要条件.
” 成立的充分不必要条件.
不正确的是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com