
已知命题p:“?x∈[1,2], x2-a≥0”与命题q:“?x∈R,x2+2ax-8-6a=0”都是真命题,则a的取值范围为_________.
x2-a≥0”与命题q:“?x∈R,x2+2ax-8-6a=0”都是真命题,则a的取值范围为_________.
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:填空题
在下列命题中,所有正确命题的序号是 .
①三点确定一个平面;②两个不同的平面分别经过两条平行直线,则这两个平面互相平行;③过高的中点且平行于底面的平面截一棱锥,把棱锥分成上下两部分的体积之比为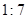 ;④平行圆锥轴的截面是一个等腰三角形.
;④平行圆锥轴的截面是一个等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下面四个命题:
①把函数 的图象向右平移
的图象向右平移 个单位,得到
个单位,得到 的图象;
的图象;
②函数 的图象在x=1处的切线平行于直线y=x,则
的图象在x=1处的切线平行于直线y=x,则 是f(x)的单调递增区间;
是f(x)的单调递增区间;
③正方体的内切球与其外接球的表面积之比为1∶3;
④“a=2”是“直线ax+2y=0平行于直线x+y=1”的充分不必要条件。
其中所有正确命题的序号为 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com