
已知f(x)=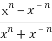 ,n∈N*,试比较f(
,n∈N*,试比较f(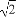 )与
)与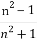 的大小,并且说明理由.
的大小,并且说明理由.
见解析
【解析】f(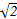 )=
)=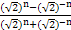 =
=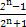
=1-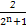 ,
,
而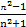 =1-
=1-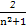 ,
,
∴f(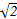 )与
)与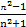 的大小等价于2n与n2的大小.
的大小等价于2n与n2的大小.
当n=1时,21>12;当n=2时,22=22;
当n=3时,23<32;当n=4时,24=42;
当n=5时,25>52.猜想当n≥5时,2n>n2.
以下用数学归纳法证明:
①当n=5时,由上可知不等式成立;
②假设n=k(k≥5,k∈N*)时,
不等式成立,即2k>k2,
则当n=k+1时,2k+1=2·2k>2k2,
又∵2k2-(k+1)2=(k-1)2-2>0(∵k≥5),即2k+1>(k+1)2,
∴n=k+1时,不等式成立.
综合①②对n≥5,n∈N*不等式2n>n2成立.
∴当n=1或n≥5时,f(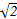 )>
)>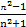 ;
;
当n=3时,f(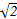 )<
)<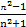 ;
;
当n=2或4时,f(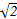 )=
)=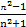 .
.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十五第十章第二节练习卷(解析版) 题型:选择题
2012年山东文博会期间,某班有甲、乙、丙、丁四名学生参加了志愿者服务工作.将这四名学生分配到A,B,C三个不同的展馆服务,每个展馆至少分配一人.若甲要求不到A馆,则不同的分配方案有( )
(A)36种 (B)30种 (C)24种 (D)20种
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:填空题
甲、乙两颗卫星同时监测台风,在同一时刻,甲、乙两颗卫星准确预报台风的概率分别为0.8和0.75,则在同一时刻至少有一颗卫星预报准确的概率为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十一第九章第二节练习卷(解析版) 题型:解答题
某中学举行了为期3天的新世纪体育运动会,同时进行全校精神文明擂台赛.为了解这次活动在全校师生中产生的影响,分别在全校500名教职员工、3000名初中生、4000名高中生中作问卷调查,如果要在所有答卷中抽出120份用于评估.
(1)应如何抽取才能得到比较客观的评价结论?
(2)要从3000份初中生的答卷中抽取一个容量为48的样本,如果采用简单随机抽样,应如何操作?
(3)为了从4000份高中生的答卷中抽取一个容量为64的样本,如何使用系统抽样抽取到所需的样本?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十一第九章第二节练习卷(解析版) 题型:选择题
某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查.现将800名学生从1到800进行编号.已知从33~48这16个数中取的数是39,则在第1小组1~16中随机抽到的数是( )
(A)5 (B)7 (C)11 (D)13
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业八十一选修4-5第三节练习卷(解析版) 题型:解答题
已知正数x,y,z满足5x+4y+3z=10.
(1)求证: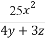 +
+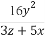 +
+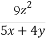 ≥5.
≥5.
(2)求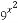 +
+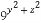 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十第八章第一节练习卷(解析版) 题型:选择题
已知直线l1:k1x+y+1=0与直线l2:k2x+y-1=0,那么“k1=k2”是“l1∥l2”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十八第八章第九节练习卷(解析版) 题型:选择题
已知任意k∈R,直线y-kx-1=0与椭圆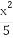 +
+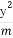 =1恒有公共点,则实数m的取值范围是( )
=1恒有公共点,则实数m的取值范围是( )
(A)(0,1) (B)(0,5)
(C)[1,5)∪(5,+∞) (D)[1,5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com