
 中,
中, 是边长为
是边长为 的正三角形,平面
的正三角形,平面 ⊥平面
⊥平面 ,
, ,
, 、
、 分别为
分别为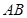 、
、 的中点.
的中点.
 ⊥
⊥ ;
;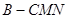 的体积.
的体积.  .
. ⊥
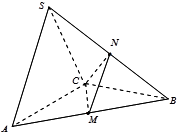
⊥ ,证明两线垂直,只需证明一线垂直另一线所在的平面,从图上看现有的平面都不满足,需重新构造,注意到
,证明两线垂直,只需证明一线垂直另一线所在的平面,从图上看现有的平面都不满足,需重新构造,注意到 ,
, 是边长为
是边长为 的正三角形,可考虑取
的正三角形,可考虑取 中点
中点 ,连结
,连结 ,
, ,这样易证
,这样易证 平面
平面 ,从而可得
,从而可得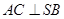 ;(Ⅱ)求三棱锥
;(Ⅱ)求三棱锥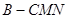 的体积,在这里
的体积,在这里 的面积不容易求,且B到平面
的面积不容易求,且B到平面 的距离也不易求,故可等体积转化,换为求三棱锥
的距离也不易求,故可等体积转化,换为求三棱锥 的体积,由题意,
的体积,由题意, ,
, 为
为 的中点,故
的中点,故 到平面
到平面 的距离就等于点
的距离就等于点 到平面
到平面 的距离的
的距离的 ,从而可得三棱锥
,从而可得三棱锥 的体积.
的体积. 中点
中点 ,连结
,连结 ,
, .
. ,∴
,∴  . 2分
. 2分 是正三角形, ∴
是正三角形, ∴ .
.  ,
, ⊥平面
⊥平面 . 4分
. 4分 在平面
在平面 内,∴
内,∴ ⊥
⊥ . 6分
. 6分
 是
是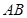 的中点,
的中点, . 8分
. 8分 ⊥平面
⊥平面 ,
, ,∴
,∴ 平面
平面 .
. ,
, ,∴
,∴ ,即点
,即点 到平面
到平面 的距离为1.
的距离为1. 是
是 的中点,∴点
的中点,∴点 到平面
到平面 的距离为
的距离为 . 10分
. 10分 . 12分
. 12分

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com