
如下图:设
a、b是异面直线,A∈a,B∈b,AB⊥a,AB⊥b,过AB的中点O作平面α与a、b分别平行,M、N分别是a、b上任意两点,MN与α交于点P,求证:
P是MN的中点.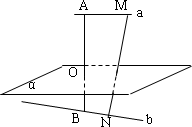
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:044
(2005
山东,22)如下图,已知动圆过定点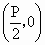 ,且与直线
,且与直线 相切,其中p>0,
相切,其中p>0,
(1)
求动圆圆心的轨迹C的方程;(2)
设A、B是轨迹C上异于原点O的两个不同点,直线OA和OB的倾斜角分别为α和β,当α、β变化且α+β为定值θ(0<θ<π)时,证明:直线AB恒过定点,并求出该定点的坐标.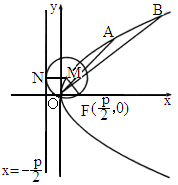
查看答案和解析>>
科目:高中数学 来源: 题型:
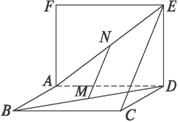
①AD⊥MN ② MN∥面CDE ③MN∥CE ④MN、CE是异面直线
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com