解:(I)设椭圆方程为

(a>b>0),F(c,0)
则直线AB的方程为y=-x+c,代入

,
化简得(a
2+b
2)x
2-2a
2cx+a
2c
2-a
2b
2=0.
令A(x
1,y
1),B(x
2,y
2),
则x
1+x
2=
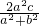
,x
1x
2=
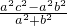
.
∵

+

=(x
1+x2,y
1+y
2),且直线x-3y+4=0的方向向量

=(3,1),

+

与

共线,
∴3(y
1+y
2)-(x
1+x
2)=0,又y
1=-x
1+c,y
2=-x
2+c,
∴3(-x
1-x
2+2c)-(x
1+x
2)=0,
∴x
1+x
2=

c.
即
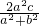
=

c,
所以a
2=3b
2.
∴c=
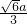
,
故离心率e=

=

.
(II)由(I)知a
2=3b
2,
所以椭圆可化为x
2+3y
2=3b
2,F(c,0),
设M(x,y),
由已知
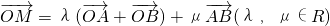
,
∴
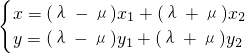
∵M(x,y)在椭圆上,即(λ-μ)
2(x
12+3y
12)+2(λ
2-μ
2)(x
1x
2+3y
1y
2)+(λ+μ)
2(x
22+3y
22)=3b
2.①
由(I)知a
2=

c
2,b
2=

c
2.
∴x
1+x
2=
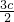
,x
1x
2=
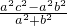
=

c
2∴x
1x
2+3y
1y
2=x
1x
2+3(-x
1+c)(-x
2+c)=4x
1x
2-3(x
1+x
2)c+3c
2=

c
2-

c
2+3c
2=0.
又x
12+3y
12=3b
2,x
22+3y
22=3b
2,
代入①得λ
2+μ
2=

.
故N的轨迹方程为λ
2+μ
2=

.
分析:(Ⅰ)直线与椭圆方程联立用未达定理的A、B两点坐标的关系,据向量共线的条件得椭圆中a,b,c的关系,从而求得椭圆的离心率;
(Ⅱ)用向量运算将λ,μ用坐标表示,再用坐标的关系求出λ
2+μ
2的值,即得N的轨迹方程.
点评:考查向量共线为圆锥曲线提供已知条件;处理直线与圆锥曲线位置关系常用的方法是直线与圆锥曲线方程联立用韦达定理.是高考常见题型且是解答题.

 的平行.
的平行.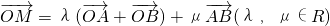 ,求N的轨迹方程.
,求N的轨迹方程. (a>b>0),F(c,0)
(a>b>0),F(c,0) ,
,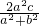 ,x1x2=
,x1x2=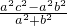 .
. +
+ =(x1+x2,y1+y2),且直线x-3y+4=0的方向向量
=(x1+x2,y1+y2),且直线x-3y+4=0的方向向量 =(3,1),
=(3,1), +
+ 与
与 共线,
共线, c.
c.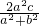 =
= c,
c,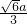 ,
, =
= .
.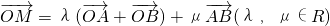 ,
,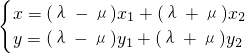
 c2,b2=
c2,b2= c2.
c2.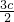 ,x1x2=
,x1x2=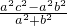 =
= c2
c2 c2-
c2- c2+3c2=0.
c2+3c2=0. .
. .
.

 阅读快车系列答案
阅读快车系列答案 已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.