
已知半径为10的圆O中,弦AB的长为10.
(1)求弦AB所对的圆心角α的大小;
(2)求α所在的扇形的弧长l及弧所在的弓形的面积S.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
已知函数f(x)=ex-1,g(x)=-x2+4x-3.若有f(a)=g(b),则b的取值范围为( ).
A.[2-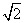 ,2+
,2+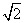 ] B.(2-
] B.(2-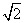 ,2+
,2+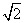 )
)
C.[1,3] D.(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知△ABC的面积S满足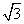 ≤S≤3,且
≤S≤3,且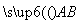 ·
·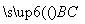 =6,设
=6,设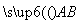 与
与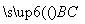 的夹角为θ.
的夹角为θ.
(1)求θ的取值范围;
(2)求函数f(θ)=sin2θ+2sin θ·cos θ+3cos2θ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
为了考察两个变量 和
和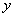 之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为
之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为 和
和 ,已知两人在试验中发现对变量
,已知两人在试验中发现对变量 的观测数据的平均值都是
的观测数据的平均值都是 ,对变量
,对变量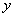 的观测数据的平均值都是
的观测数据的平均值都是 ,那么下列说法正确的是( )
,那么下列说法正确的是( )
A. 和
和 有交点
有交点 B.
B. 与
与 相交,但交点不一定是
相交,但交点不一定是
C. 与
与 必定平行 D.
必定平行 D. 与
与 必定重合
必定重合
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数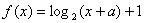 过点
过点 .
.
(1)求实数 ;
;
(2)将函数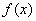 的图象向下平移1个单位,再向右平移
的图象向下平移1个单位,再向右平移 个单位后得到函数
个单位后得到函数 图象,设函数
图象,设函数 关于
关于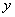 轴对称的函数为
轴对称的函数为 ,试求
,试求 的解析式;
的解析式;
(3)对于定义在 上的函数
上的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com