
【题目】已知抛物线![]() 经过点
经过点![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]() ,且直线
,且直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)设![]() 为原点,
为原点,![]() ,求证:
,求证:![]() 为定值.
为定值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C的方程为![]() ,设AB是过椭圆C中心O的任意弦,l是线段AB的垂直平分线,M是l上与O不重合的点.
,设AB是过椭圆C中心O的任意弦,l是线段AB的垂直平分线,M是l上与O不重合的点.
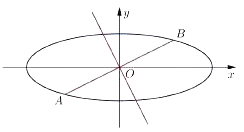
(1)求以椭圆的焦点为顶点,顶点为焦点的双曲线方程;
(2)若![]() ,当点A在椭圆C上运动时,求点M的轨迹方程;
,当点A在椭圆C上运动时,求点M的轨迹方程;
(3)记M是l与椭圆C的交点,若直线AB的方程为![]() ,当
,当![]() 面积取最小值时,求直线AB的方程;
面积取最小值时,求直线AB的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() (
(![]() ).
).
(1)当![]() 时,解关于
时,解关于![]() 的方程
的方程![]() (其中
(其中![]() 为自然对数的底数);
为自然对数的底数);
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由. (参考数据:
的最小值;若不存在,请说明理由. (参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某芯片公司对今年新开发的一批5G手机芯片进行测评,该公司随机调查了100颗芯片,并将所得统计数据分为![]() 五个小组(所调查的芯片得分均在
五个小组(所调查的芯片得分均在![]() 内),得到如图所示的频率分布直方图,其中
内),得到如图所示的频率分布直方图,其中![]() .
.
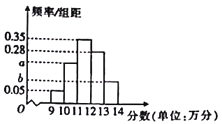
(1)求这100颗芯片评测分数的平均数(同一组中的每个数据可用该组区间的中点值代替).
(2)芯片公司另选100颗芯片交付给某手机公司进行测试,该手机公司将每颗芯片分别装在3个工程手机中进行初测。若3个工程手机的评分都达到11万分,则认定该芯片合格;若3个工程手机中只要有2个评分没达到11万分,则认定该芯片不合格;若3个工程手机中仅1个评分没有达到11万分,则将该芯片再分别置于另外2个工程手机中进行二测,二测时,2个工程手机的评分都达到11万分,则认定该芯片合格;2个工程手机中只要有1个评分没达到11万分,手机公司将认定该芯片不合格.已知每颗芯片在各次置于工程手机中的得分相互独立,并且芯片公司对芯片的评分方法及标准与手机公司对芯片的评分方法及标准都一致(以频率作为概率).每颗芯片置于一个工程手机中的测试费用均为300元,每颗芯片若被认定为合格或不合格,将不再进行后续测试,现手机公司测试部门预算的测试经费为10万元,试问预算经费是否足够测试完这100颗芯片?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆市的新高考模式为“![]() ”,其中“3”是指语文、数学、外语三门必步科目:“1”是指物理、历史两门科目必选且只选一门;“2”是指在政治、地理、化学、生物四科中必须任选两门,这样学生的选科就可以分为两类:物理类与历史类,比如物理类有:物理+化学+生物,物理+化学+地理,物理+化学+政治.物理+政治+地理,物理+政治+生物,物理+生物+地理.重庆某中学高一学生共1200人,其中男生650人,女生550人,为了适应新高考,该校高一的学生在3月份进行了“
”,其中“3”是指语文、数学、外语三门必步科目:“1”是指物理、历史两门科目必选且只选一门;“2”是指在政治、地理、化学、生物四科中必须任选两门,这样学生的选科就可以分为两类:物理类与历史类,比如物理类有:物理+化学+生物,物理+化学+地理,物理+化学+政治.物理+政治+地理,物理+政治+生物,物理+生物+地理.重庆某中学高一学生共1200人,其中男生650人,女生550人,为了适应新高考,该校高一的学生在3月份进行了“![]() ”的选科,选科情况部分数据如下表所示:(单位:人)
”的选科,选科情况部分数据如下表所示:(单位:人)
性别 | 物理类 | 历史类 | 合计 |
男生 | 590 | ||
女生 | 240 | ||
合计 | 900 |
(1)请将题中表格补充完整,并判断能否有99%把握认为“是否选择物理类与性别有关”?
(2)已知高一9班和10班选科结果都只有四种组合:物理+化学+生物,物理+化学+地理,政治+历史+地理,政治+历史+生物.现用数字1,2,3,4依次代表这四种组合,两个班的选科数据如下表所示(单位:人).
理化生 | 理化地 | 政史地 | 政史生 | 班级总人数 | |
9班 | 18 | 18 | 12 | 12 | 60 |
10班 | 24 | 12 | 18 | 6 | 60 |
现分别从两个班各选一人,记他们的选科结果分别为![]() 和
和![]() ,令
,令![]() ,用频率代表概率,求随机变量
,用频率代表概率,求随机变量![]() 的分布列和期望.(参考数据:
的分布列和期望.(参考数据:![]() ,
,![]() ,
,![]() )
)
附: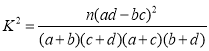 ;
;
| 0.050 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
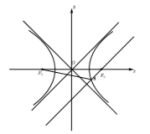
【题目】如图,已知双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,过右焦点作平行于一条渐近线的直线交双曲线于点
,过右焦点作平行于一条渐近线的直线交双曲线于点![]() ,若
,若![]() 的内切圆半径为
的内切圆半径为![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】九龙坡区围绕大力发展高新技术产业、推进高质量城市管理、创造高品质人民生活,建设宜居、宜业、宜游的“三高九龙坡、三宜山水城”的总愿景,全面开启新时代的新梦想、新征程.热心网友“我是坡民”通过问卷,对近五年游客满意度排在前三名的区内景点进行了统计,结果如表一.根据此表,他又对游览过热门景点重庆动物园的100名游客进行满意度调查,给景点打分,满分为100分,得分超过90分的为“特别满意”,其余为“基本满意”,将受调查游客年龄为12岁及以下的人群称为儿童,得到![]() 列联表,如表二:
列联表,如表二:
表一:
年份景点排名 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
1 | 重庆动物园 | 重庆动物园 | 龙门阵景区 | 彩云湖 | 彩云湖 |
2 | 华岩景区 | 华岩景区 | 重庆动物园龙 | 龙门阵景区 | 黄桷坪涂鸦街 |
3 | 巴国城 | 海兰云天 | 黄桷坪涂鸦街 | 华岩景区 | 重庆动物园 |
表二:
特别满意 | 基本满意 | 合计 | |
儿童 | 40 | ||
非儿童 | 30 | ||
合计 | 60 | 100 |
(1)完成表二的列联表,并判断是否有99.9%的把握认为调查对象是否“特别满意”与是否是儿童有关;
(2)为安排节假日出行,“我是坡民”从表一的5个年份中随机选择2个年份,再从这2个年份排名前三的景点中任意选择1个景点,记选择出的景点中“重庆动物园”出现的次数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 经过曲线
经过曲线![]() 的焦点
的焦点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com