
【题目】已知函数f(x)=(ax-2)ex在x=1处取得极值.
(1)求a的值;
(2)求函数在区间[m,m+1]上的最小值.
【答案】(1)1(2)f(x)min=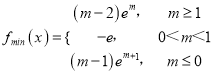 .
.
【解析】
(1)f′(x)=aex+(ax﹣2)ex=(ax+a﹣2)ex,由此利用导数性质能求出a=1.
(2)由f(x)=(x﹣2)ex,得f′(x)=ex+(x﹣2)ex=(x﹣1)ex.由f′(x)=0,得x=1,由此列表讨论,能求出f(x)在[m,m+1]上的最小值.
解 (1)f′(x)=(ax+a-2)ex,
由已知得f′(1)=(a+a-2)e=0,
解得a=1,经检验a=1符合题意,
所以a的值为1.
(2)由(1)得f(x)=(x-2)ex,f′(x)=(x-1)ex.
令f′(x)>0得x>1,令f′(x)<0得x<1.
所以函数f(x)在(-∞,1)上递减,在(1,+∞)上递增.
当m≥1时,f(x)在[m,m+1]上递增,f(x)min=f(m)=(m-2)em,
当0<m<1时,f(x)在[m,1]上递减,在(1,m+1]上递增,f(x)min=f(1)=-e.
当m≤0时,m+1≤1,f(x)在[m,m+1]上单调递减,
f(x)min=f(m+1)=(m-1)em+1.
综上,f(x)在[m,m+1]上的最小值为
f(x)min=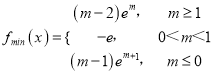 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(a>b>0)的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点Q(4,0)且不与坐标轴垂直的直线l交椭圆C于A、B两点,设点A关于x轴的对称点为A1.求证:直线A1B过x轴上一定点,并求出此定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知椭圆![]() :
:![]() 的左、右顶点分别为A,B,其离心率
的左、右顶点分别为A,B,其离心率![]() ,点
,点![]() 为椭圆上的一个动点,
为椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若过椭圆![]() 右顶点
右顶点![]() 的直线
的直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区随着经济的发展,居民收入逐年增长,银行储蓄连年增长,下表是该地区某银行连续五年的储蓄存款(年底结算):
年份 |
|
|
|
|
|
储蓄存款 |
|
|
|
|
|
为方便研究,工作人员对上表的数据做了如下处理:![]() ,
,![]() 得到下表:
得到下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的线性回归方程,并用所求回归方程预测
的线性回归方程,并用所求回归方程预测![]() 年底,该地储蓄存款额可达多少?
年底,该地储蓄存款额可达多少?
(附:参考公式![]() ,其中
,其中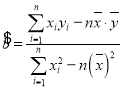 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的函数f(x)满足f(x)+f′(x)>1,f(0)=4,则不等式f(x)>![]() +1(e为自然对数的底数)的解集为( )
+1(e为自然对数的底数)的解集为( )
A.(0,+∞)B.(-∞,0)∪(3,+∞)
C.(-∞,0)∪(0,+∞)D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 是圆
是圆![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上点,且
上点,且![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,与圆
两点,与圆![]() 相交于另一点
相交于另一点![]() ,且点
,且点![]() 、
、![]() 位于点
位于点![]() 的同侧,当
的同侧,当![]() 面积最大时,求
面积最大时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com