
(本小题满分12分)如图,四棱锥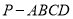 的底面ABCD是平行四边形,
的底面ABCD是平行四边形,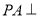 底面ABCD,
底面ABCD,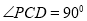 ,
,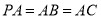 .
.
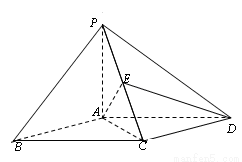
(1)求证: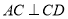 ;
;
(2)点E在棱PC上,满足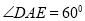 ,求二面角
,求二面角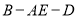 的余弦值.
的余弦值.
(1)证明详见解析;(2)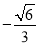 .
.
【解析】
试题分析:本题主要考查线线垂直、线面垂直、二面角、向量法等基础知识,同时考查分析问题解决问题的能力、推理论证能力、运算求解能力. 第一问,利用线面垂直“PA⊥底面ABCD”的性质可得PA⊥CD,而PC⊥CD,则利用线面垂直的判定可得CD⊥平面PAC,所以CD垂直于面PAC内的线;第二问,根据已知条件得到AB、AC、AP两两垂直,建立空间直角坐标系,写出相应点和相应向量的坐标,利用夹角的余弦公式解出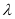 ,再求
,再求 的值.
的值.
试题解析:(Ⅰ)证明:
因为PA⊥底面ABCD,所以PA⊥CD,
因为∠PCD=90,所以PC⊥CD,
所以CD⊥平面PAC,
所以CD⊥AC. 4分
(Ⅱ)
因为底面ABCD是平行四边形,CD⊥AC,所以AB⊥AC.又PA⊥底面ABCD,所以AB,AC,AP两两垂直.
如图所示,以点A为原点,以 为x轴正方向,以
为x轴正方向,以 为单位长度,建立空间直角坐标系.
为单位长度,建立空间直角坐标系.

则B(1,0,0),C(0,1,0),P(0,0,1),D(-1,1,0).
设 ,则
,则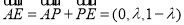 ,
,
又∠DAE=60°,则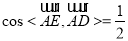 ,
,
即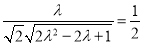 ,解得
,解得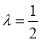 . 8分
. 8分
则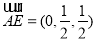 ,
,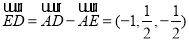 ,
,
所以 .
.
因为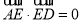 ,所以
,所以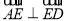 .又
.又 ,
,
故二面角B-AE-D的余弦值为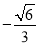 . 12分
. 12分
考点:线线垂直、线面垂直、二面角、向量法.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源:2014-2015学年江苏省宿迁市高三上学期第一次摸底考试文科数学试卷(解析版) 题型:解答题
如图,在四棱锥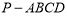 中,底面
中,底面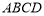 是菱形,且
是菱形,且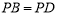 .
.

(1)求证: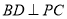 ;
;
(2)若平面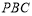 与平面
与平面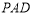 的交线为
的交线为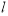 ,求证:
,求证: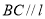 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北唐山市高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为 ,斜率为
,斜率为 的直线
的直线 交y轴于点
交y轴于点 .
.
(1)求C的直角坐标方程, 的参数方程;
的参数方程;
(2)直线 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求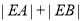 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北唐山市高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系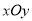 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为 ,斜率为
,斜率为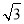 的直线
的直线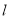 交y轴于点
交y轴于点 .
.
(1)求C的直角坐标方程,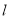 的参数方程;
的参数方程;
(2)直线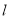 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
在平面直角坐标系中,一条双曲线经过旋转或平移所产生的一系列双曲线都具有相同的离心率和焦距,称它们为一组“共性双曲线”;例如将等轴双曲线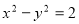 绕原点逆时针转动
绕原点逆时针转动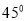 ,就会得到它的一条“共性双曲线”
,就会得到它的一条“共性双曲线”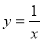 ;根据以上材料可推理得出双曲线
;根据以上材料可推理得出双曲线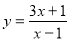 的焦距为( )
的焦距为( )
A.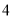 B.
B.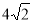 C.
C.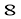 D.
D.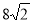
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com