B
分析:依题意,不妨设过其右焦点F的直线的斜率为1,利用双曲线的第二定义可求得可求得|PQ|,继而可求得PQ的垂直平分线方程,令x=0可求得点M的横坐标,从而使问题解决.
解答:∵双曲线的方程为

-

=1,
∴其右焦点F(5,0),不妨设过其右焦点F的直线的斜率为1,
依题意,直线PQ的方程为:y=x-5.
由
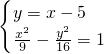
得:7x
2+90x-369=0,
设P(x
1,y
1),Q(x
2,y
2),则x
1,x
2为方程7x
2+90x-369=0的两根,
∴x
1+x
2=-

,y
1+y
2=(x
1-5)+(x
2-5)=x
1+x
2-10=-
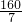
,
∴线段PQ的中点N(-
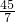
,-

),
∴PQ的垂直平分线方程为y+

=-(x+
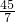
),
令y=0得:x=-

.又右焦点F(5,0),
∴|MF|=5+

=
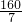
.①
设点P在其准线上的射影为P′,点Q在其准线上的射影为Q′,
∵双曲线的一条渐近线为y=

x,其斜率k=

,直线PQ的方程为:y=x-5,其斜率k′=1,
∵k′<k,
∴直线PQ与双曲线的两个交点一个在左支上,另一个在右支上,不妨设点P在左支,点Q在右支,
则由双曲线的第二定义得:

=
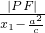
=e=

=

,
∴|PF|=

x
1-

×
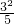
=

x
1-3,
同理可得|QF|=3-

x
2;
∴|PQ|=|QF|-|PF|
=3-

x
2-(

x
1-3)
=6-

(x
1+x
2)
=6-

×(-

)
=

.②
∴
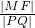
=

=

.
故选B.
点评:本题考查双曲线的第二定义的应用,考查直线与圆锥曲线的相交问题,考查韦达定理的应用与直线方程的求法,综合性强,难度大,属于难题.

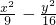 =1,过其右焦点F的直线(斜率存在)交双曲线于P、Q两点,PQ的垂直平分线交x轴于点M,则
=1,过其右焦点F的直线(斜率存在)交双曲线于P、Q两点,PQ的垂直平分线交x轴于点M,则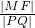 的值为
的值为



 -
- =1,
=1,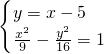 得:7x2+90x-369=0,
得:7x2+90x-369=0, ,y1+y2=(x1-5)+(x2-5)=x1+x2-10=-
,y1+y2=(x1-5)+(x2-5)=x1+x2-10=-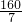 ,
,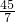 ,-
,- ),
), =-(x+
=-(x+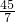 ),
), .又右焦点F(5,0),
.又右焦点F(5,0), =
=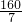 .①
.① x,其斜率k=
x,其斜率k= ,直线PQ的方程为:y=x-5,其斜率k′=1,
,直线PQ的方程为:y=x-5,其斜率k′=1, =
=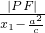 =e=
=e= =
= ,
, x1-
x1- ×
×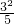 =
= x1-3,
x1-3, x2;
x2; x2-(
x2-( x1-3)
x1-3) (x1+x2)
(x1+x2) ×(-
×(- )
) .②
.②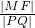 =
= =
= .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 =1,过其右焦点F的直线(斜率存在)交双曲线于P、Q两点,PQ的垂直平分线交x轴于点M,则
=1,过其右焦点F的直线(斜率存在)交双曲线于P、Q两点,PQ的垂直平分线交x轴于点M,则 的值为( )
的值为( )


