
已知抛物线y2=-x与直线y=k(x+1)交于A、B两点.
(1)求证:OA⊥OB;
(2)当DAOB的面积等于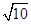 时,求k的值.
时,求k的值.
(1)证明见试题解析;(2)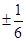 .
.
【解析】
试题分析:(1)要证明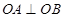 ,可设出
,可设出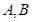 两点的坐标分别为
两点的坐标分别为 ,则
,则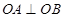
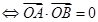
 ,而
,而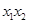 ,
,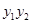 从哪里来呢?考虑到
从哪里来呢?考虑到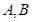 两点在抛物线上,因此
两点在抛物线上,因此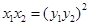 ,下面的目标是求
,下面的目标是求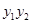 ,我们把直线方程与抛物线方程联立,消去
,我们把直线方程与抛物线方程联立,消去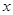 ,得到关于
,得到关于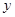 的二次方程,
的二次方程, 正是这个二次方程的解,利用韦达定理,可得
正是这个二次方程的解,利用韦达定理,可得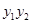 ,从而证得结论;(2)如果直接利用
,从而证得结论;(2)如果直接利用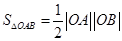 ,则
,则 ,会发现很难把这个根式用
,会发现很难把这个根式用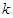 表示出来,我们换一种思路,直线
表示出来,我们换一种思路,直线 交
交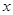 轴于点
轴于点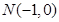 ,因此
,因此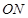 把
把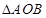 分成两个三角形,从而有
分成两个三角形,从而有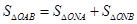
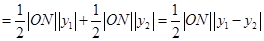 ,这里
,这里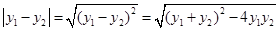 ,正好能利用(1)结论中的结论.
,正好能利用(1)结论中的结论.
试题解析:(1)由方程组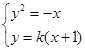 得:
得: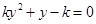 ,
,
设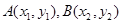 ,由韦达定理得:
,由韦达定理得: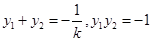 ,
,
∴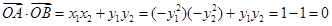 ,
,
∴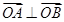 ,即
,即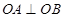 .4分
.4分

(2)设直线与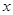 交于
交于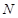 点,则
点,则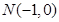 ,
,
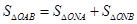
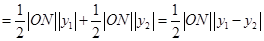
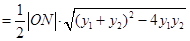
∴ ,
,
∴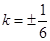 .10分
.10分
考点:(1)直线与抛物线相交,垂直问题;(2)面积问题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源:北京市西城区2012届高三4月第一次模拟考试数学文科试题 题型:022
如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….

给出下列三个结论:
①数列{yn}是递减数列;
②对![]() n∈N*,yn>0;
n∈N*,yn>0;
③若y1=4,y2=3,则y5=![]() .
.
其中,所有正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源:2015届山西太原第五中学高二12月月考文科数学试卷(解析版) 题型:解答题
已知抛物线y2=-x与直线y=k(x+1)交于A、B两点.
(1)求证:OA⊥OB;
(2)当DAOB的面积等于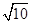 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源:2012届山东省高二上学期学业水平测试数学试卷 题型:解答题
已知抛物线y2=-x与直线y=k(x+1)相交于A、B两点.
(Ⅰ)求证:OA⊥OB;
(Ⅱ)当△OAB的面积等于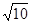 时,求k的值.
时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com