
分析 利用直译法,求①选项中动点P的轨迹方程,进而判断表示的曲线;利用新定义运算,利用直译法求选项②中曲线的轨迹方程,进而判断轨迹图形;利用圆与圆的位置关系,利用定义法判断选项③中动点的轨迹;
利用椭圆定义,由定义法判断④中动点的轨迹即可.
解答 解:设P(x,y),因为直线PA、PB的斜率存在,所以x≠±4,直线PA、PB的斜率分别是k1=$\frac{y}{x+4}$,k2=$\frac{y}{x-4}$,∴$\frac{y}{x+4}•\frac{y}{x-4}=\frac{4}{9}$,化简得9y2=4x2-64,即$\frac{{x}^{2}}{16}-\frac{9{y}^{2}}{64}=1$(x≠±4),
∴动点P的轨迹为双曲线的一部分,①正确;
∵m*n=(m+n)2-(m-n)2,∴$\sqrt{x*a}$=2$\sqrt{ax}$,设P(x,y),则y=2$\sqrt{ax}$,即y2=4ax(x≥0,y≥0),即动点$P(x,\sqrt{x*a})$的轨迹是抛物线的一部分,②正确;
由题意可知,动圆M与定圆A相外切与定圆B相内切
∴MA=r+1,MB=5-r
∴MA+MB=6>AB=2
∴动圆圆心M的轨迹是以A,B为焦点的椭圆,③正确;
设此椭圆的另一焦点的坐标D (x,y),
∵椭圆过A、B两点,则 CA+DA=CB+DB,
∴15+DA=13+DB,∴DB-DA=2<AB,
∴椭圆的另一焦点的轨迹是以A、B为焦点的双曲线一支,④错误
故答案为:①②③.
点评 本题综合考查了求动点轨迹的两种方法:直译法和定义法,考查了圆、椭圆、抛物线、双曲线的定义,椭圆、双曲线、抛物线的标准方程,有一定难度.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x3 | B. | f(x)=x${\;}^{\frac{1}{2}}$ | C. | f(x)=3x | D. | f(x)=($\frac{1}{2}$)x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
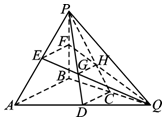 已知:在三棱锥P-ABQ 中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则多面体ADGE-BCHF的体积与三棱锥P-ABQ体积之比是$\frac{11}{18}$.
已知:在三棱锥P-ABQ 中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则多面体ADGE-BCHF的体积与三棱锥P-ABQ体积之比是$\frac{11}{18}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [ln2,ln$\frac{3}{2}$+$\frac{1}{3}$] | B. | (ln2,ln$\frac{3}{2}$+$\frac{1}{3}$) | C. | ($\frac{2}{3}$,ln2] | D. | ($\frac{2}{3}$,ln$\frac{3}{2}$+$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①②③④ | C. | ②③④⑤ | D. | ③④⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com