
【题目】已知![]() ,
,![]() .
.
(1)若![]() ,命题“p∨q”为真,求实数
,命题“p∨q”为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1)[﹣4,2);(2) [﹣4,1]
【解析】
(1)根据复合命题真假关系进行转化求当命题“p∨q”为假时的范围即可.
(2)根据必要不充分条件与集合包含关系进行转化求解即可.
(1)若m=2时,p:﹣4≤x≤1,q:﹣1<x<2,
p∨q为真时,p、q两个命题一真一假或两个都为真,其对立事件为两个都为假,当p假且q假时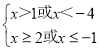 ,即x≥2或x<﹣4,
,即x≥2或x<﹣4,
所以p∨q为真时﹣4≤x<2,即x的取值范围为[﹣4,2);
(2)若p是q的必要不充分条件,则q的解集![]() p的解集,
p的解集,
①q=时,即m=﹣1时,满足题意;
②q≠时,当m>﹣1时p:﹣4≤x≤1,q:﹣1<x<m,因为q的解集![]() p的解集,所以m≤1.即-1<m≤1
p的解集,所以m≤1.即-1<m≤1
当m<﹣1时p:﹣4≤x≤1,q:m<x<﹣1,因为q的解集![]() p的解集,所以-1>m≥﹣4.
p的解集,所以-1>m≥﹣4.
综上﹣4≤m≤1;
综上,实数m的取值范围为[﹣4,1].


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为直角梯形,
中,底面ABCD为直角梯形,![]()
![]() ,
,![]() 平面ABCD,E是棱PC上的一点.
平面ABCD,E是棱PC上的一点.
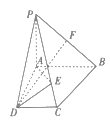
(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,F是PB的中点,
,F是PB的中点,![]() ,
,![]() ,求直线DF与平面
,求直线DF与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为
(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为![]() ,点A的坐标为
,点A的坐标为![]() ,且
,且![]() .
.
(I)求椭圆的方程;
(II)设直线l: ![]() 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若
与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若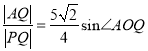 (O为原点) ,求k的值.
(O为原点) ,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为担任班主任的教师办理手机语音月卡套餐,为了解通话时长,采用随机抽样的方法,得到该校100位班主任每人的月平均通话时长![]() (单位:分钟)的数据,其频率分布直方图如图所示,将频率视为概率.
(单位:分钟)的数据,其频率分布直方图如图所示,将频率视为概率.
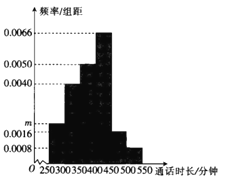
(1)求图中![]() 的值;
的值;
(2)估计该校担任班主任的教师月平均通话时长的中位数;
(3)在![]() ,
,![]() 这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.
这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com