Question

已知点F₁（-4，0），F₂（4，0），又P（x，y）是曲线上的点，则（ ）
A．|PF₁|+|PF₂|=10
B．|PF₁|+|PF₂|＜10
C．|PF₁|+|PF₂|≤10
D．|PF₁|+|PF₂|≥10

Answer 1

【答案】分析：法一：根据方程，可以联想椭圆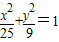，根据椭圆的定义可知，是以点F₁（-4.0），F₂（4，0）为焦点的椭圆，在椭圆上任意取点，可以证明点在曲线的内部或在曲线上，即椭圆上的点在封闭曲线的内部或曲线上，故可得结论．
法二：任取点P（x，y）在曲线上，可令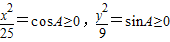，A∈[0，]，易证得sinA+cosA≥1，即由此知点P（x，y）在上可其外部，再由椭圆的定义易选出正确选项
解答：解：根据方程，可以联想椭圆，
在椭圆上取点Q（5cosα，3sinα），即x=5cosα，y=3sinα
则=2
∵0≤sin²α≤1，
∴
即点Q在曲线的内部或在曲线上
所以椭圆上的点在封闭曲线的内部或曲线上
由题意，是以点F₁（-4.0），F₂（4，0）为焦点的椭圆
∴当P点恰好取在顶点上时，此时点P在椭圆上，故有|PF₁|+|PF₂|=10
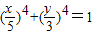点P不在曲线的顶点上时，必有点P在椭圆的外部，故|PF₁|+|PF₂|＞10
综上所述，|PF₁|+|PF₂|≥10
故选D．
法二：任取点P（x，y）在曲线上，可令，A∈[0，]
则有sinA+cosA≥1，即由此知点P（x，y）在上可其外部，故有|PF₁|+|PF₂|≥10
故选D
点评：本题以曲线为载体，考查类比思想，考查椭圆的定义，考查学生分析解决问题的能力．