
在直角坐标系 中,曲线C的参数方程为
中,曲线C的参数方程为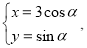 (其中
(其中 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系中,直线
轴的正半轴为极轴建立极坐标系中,直线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求C的普通方程和直线 的倾斜角;
的倾斜角;
(Ⅱ)设点 (0,2),
(0,2), 和
和 交于
交于 两点,求
两点,求 .
.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源:2015-2016学年福建省高二下期中文科数学试卷(解析版) 题型:选择题
已知椭圆 的右焦点为
的右焦点为 是椭圆上一点,点
是椭圆上一点,点 ,当
,当 的周长最大时,直线
的周长最大时,直线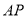 的方程为( )
的方程为( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届山西省等四校高三下第四次联考文科数学试卷(解析版) 题型:解答题
某研究性学习小组对4月份昼夜温差大小与花卉种子发芽多少之间的关系研究,记录了4月1日至4月5日的每天昼夜温差与实验室每天100颗种子浸泡后的发芽数,如下表:

(Ⅰ)请根据上表中4月2日至4月4日的数据,求出y关于x的线性回归方程 ;若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,请用4月1日和4月5日数据检验你所得的线性回归方程是否可靠?
;若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,请用4月1日和4月5日数据检验你所得的线性回归方程是否可靠?
(Ⅱ)从4月1日至4月5日中任选2天,记发芽的种子数分别为 ,求事件“m ,n均不小于25”的概率.
,求事件“m ,n均不小于25”的概率.
(参考公式:回归直线的方程是 ,其中
,其中 ,
, )
)
查看答案和解析>>
科目:高中数学 来源:2016届山西省等四校高三下第四次联考文科数学试卷(解析版) 题型:选择题
已知双曲线 的左右焦点分别为
的左右焦点分别为 ,
, ,若
,若 上存在点
上存在点 使
使 为等腰三角形,且其顶角为
为等腰三角形,且其顶角为 ,则
,则 的值是( )
的值是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届山西省等四校高三下第四次联考理科数学试卷(解析版) 题型:解答题
根据国家《环境空气质量标准》规定:居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称可入肺颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:

(1)写出该样本的众数和中位数(不必写出计算过程);
(2)求该样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由;
(3)将频率视为概率,对于去年的某2天,记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为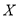 ,求
,求 的分布列及数学期望
的分布列及数学期望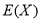 和方差
和方差 .
.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二下期中文科数学试卷(解析版) 题型:解答题
已知抛物线 的顶点在坐标原点
的顶点在坐标原点 ,其图像关于
,其图像关于 轴对称且经过点
轴对称且经过点 .
.
(1)求抛物线 的方程;
的方程;
(2)若一个等边三角形的一个顶点位于坐标原点,另两个顶点在抛物线上,求该等边三角形的面积;
(3)过点 作抛物线
作抛物线 的两条弦
的两条弦 ,设
,设 所在直线的斜率分别为
所在直线的斜率分别为 ,当
,当 时,试证明直线
时,试证明直线 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com