
设N=2n(n∈N*,n≥2),将N个数x1,x2,…,xN依次放入编号为1,2,…,N的N个位置,得到排列P0=x1x2…xN.将该排列中分别位于奇数与偶数位置的数取出,并按原顺序依次放入对应的前 和后
和后 个位置,得到排列P1=x1x3…xN-1x2x4…xN,将此操作称为C变换,将P1分成两段,每段
个位置,得到排列P1=x1x3…xN-1x2x4…xN,将此操作称为C变换,将P1分成两段,每段 个数,并对每段作C变换,得到
个数,并对每段作C变换,得到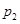 ;当2≤i≤n-2时,将Pi分成2i段,每段
;当2≤i≤n-2时,将Pi分成2i段,每段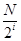 个数,并对每段C变换,得到Pi+1,例如,当N=8时,P2=x1x5x3x7x2x6x4x8,此时x7位于P2中的第4个位置.
个数,并对每段C变换,得到Pi+1,例如,当N=8时,P2=x1x5x3x7x2x6x4x8,此时x7位于P2中的第4个位置.
(1)当N=16时,x7位于P2中的第___个位置;
(2)当N=2n(n≥8)时,x173位于P4中的第___个位置.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| N |
| 2 |
| N |
| 2 |
| N |
| 2 |
| N |
| 2i |
查看答案和解析>>
科目:高中数学 来源: 题型:
| N |
| 2 |
| N |
| 2 |
| N |
| 2 |
| N |
| 2i |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x |
| 1-x |
| 1 |
| 2 |
| 1 |
| n |
| 2 |
| n |
| n-2 |
| n |
| n-1 |
| n |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com