
分析 (1)由题意利用正弦函数的图象的对称性可得φ的值.
(2)由条件利用正弦函数的单调性求得函数f(x)的单调递减区间.
(3)由条件利用正弦函数的定义域和值域,求得函数f(x)在区间[-$\frac{π}{12}$,$\frac{π}{2}$]上的值域.
解答 解:(1)由于函数f(x)=2sin(2x+φ)(-π<φ<0)图象的一个对称中心为($\frac{7π}{12}$,0),
故有2•$\frac{7π}{12}$+φ=kπ,k∈π,求得φ=-$\frac{π}{6}$,∴f(x)=2sin(2x-$\frac{π}{6}$).
(2)对于函数f(x)=2sin(2x-$\frac{π}{6}$),令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,
求得kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$,可得函数的减区间为[kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$],k∈Z.
(3)∵x∈[-$\frac{π}{12}$,$\frac{π}{2}$],∴2x-$\frac{π}{6}$∈[-$\frac{π}{3}$,$\frac{5π}{6}$],∴sin(2x-$\frac{π}{6}$)∈[-$\frac{\sqrt{3}}{2}$,1],
故函数的值域为[-$\sqrt{3}$,2]..
点评 本题主要考查正弦函数的图象的对称性,正弦函数的单调性,正弦函数的定义域和值域,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数 | B. | 是偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 是非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
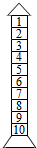 如图是某建筑物的模型,现在要给该模型进行涂色,有红,黄,蓝,绿四种颜色可用,每层只能用一种颜色,在每一层涂色时,每种颜色被使用的可能性相同.
如图是某建筑物的模型,现在要给该模型进行涂色,有红,黄,蓝,绿四种颜色可用,每层只能用一种颜色,在每一层涂色时,每种颜色被使用的可能性相同.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
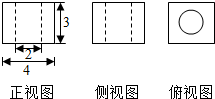 如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体的表面积是( )
如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体的表面积是( )| A. | 80-2π | B. | 80 | C. | 80+4π | D. | 80+6π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则$\overrightarrow{a}$$⊥\overrightarrow{b}$ | B. | 若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | ||
| C. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则存在实数λ使得$\overrightarrow{a}$=$λ\overrightarrow{b}$ | D. | 若存在实数λ使得$\overrightarrow{a}$=$λ\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com