
空间四边形ABCD中,AB=CD且AB与CD成60°角,点M、N分别是BC、AD的中点(如图),求直线AB和MN所成的角.

|
过 M作MP∥ΑB,连NP则 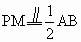 , ,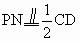 ,又AB=CD ,又AB=CD
∴ PM=PN且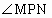 =60°或 =60°或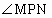 =120° =120°
∴ 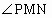 =60°或 =60°或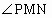 =30° =30°
故 AB与MN所成的角为60°或30°. |
|
求两条异面直线所成的角的步骤为: (1) 利用定义构造角.可固定一条,平移另一条;或两条同时平移到某个特殊位置.(2) 证明作出的角即为所求角.(3) 利用三角形求角,异面直线所成角的范围是(0°,90°].因此如果平移后,在三角形中求出的角是钝角,则取它的补角.本题可根据异面直线所成角的定义,作出异面直线 AB与CD;AB与MN所成的角.然后计算之. |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com