练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    四边形ABCD中＝2，则四边形ABCD为

    [　　]

    A．平行四边形

    B．矩形

    C．梯形

    D．菱形

    答案：C
    解析：

    ∵＝2，∴∥且||＝2||．故四边形为梯形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：101网校同步练习　高三数学　苏教版(新课标·2004年初审) 苏教版 题型：044

    四边形ABCD中＝(6，1)，＝(x，y)，＝(－2，－3)，

    (1)若∥，求x与y间的关系式；

    (2)满足(1)问的同时又有⊥，求x，y的值及四边形ABCD的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    空间四边形ABCD中，AB、BC、CD的中点分别为P、Q、R，且AC＝4，BD＝2，PR＝3，则AC和BD所成的角为(　　)

    A．90°                                 B．60° 

    C．45°                                 D．30°

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省高三高考模拟卷（二）文科数学试卷（解析版） 题型：解答题

    如图，四边形ABCD中，AB⊥AD，AD∥BC，AD＝6，BC＝4，AB＝2，E、F分别在BC、AD上，EF∥AB．现将四边形ABEF沿EF折起，使得平面ABEF平面EFDC．

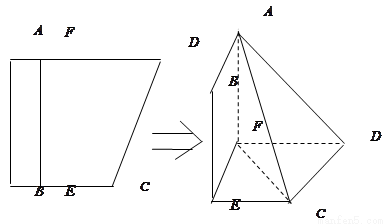
    (Ⅰ) 当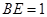，是否在折叠后的AD上存在一点，且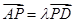，使得CP∥平面ABEF？若存在，求出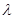的值；若不存在，说明理由；

    (Ⅱ) 设BE＝x，问当x为何值时，三棱锥A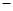CDF的体积有最大值？并求出这个最大值．

     

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学直线、平面、简单几何体专项训练（河北） 题型：解答题

    如图所示，四棱锥P－ABCD中，PD⊥平面ABCD，PA与平面ABCD所成的角为60°，在四边形ABCD中，∠D＝∠DAB＝90°，AB＝4，CD＝1，AD＝2.

    (1)建立适当的坐标系，并写出点B，P的坐标；

    (2)求异面直线PA与BC所成角的余弦值；

    (3)若PB的中点为M，求证：平面AMC⊥平面PBC.

     

    查看答案和解析>>

    同步练习册答案