
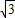 ,-1).
,-1). ]上的单调递增区间.
]上的单调递增区间.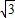 ,-1),利用任意角的三角函数的定义求得sinα、cosα、tanα 的值,即可求得
,-1),利用任意角的三角函数的定义求得sinα、cosα、tanα 的值,即可求得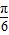 ),令 2kπ-
),令 2kπ-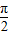 ≤2x-
≤2x-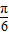 ≤2kπ+
≤2kπ+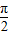 ,k∈z,
,k∈z,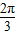 ]上的单调递增区间.
]上的单调递增区间.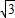 ,-1).
,-1).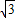 ,y=-1,r=
,y=-1,r=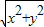 =2,∴sinα=
=2,∴sinα= =-
=- ,cosα=
,cosα=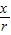 =
=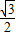 ,tanα=
,tanα=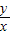 =-
=-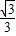 .
. )×
)×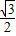 +
+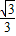 =-
=-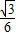 .
.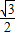 sin2x-
sin2x- cos2x=sin(2x-
cos2x=sin(2x-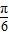 ),
),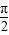 ≤2x-
≤2x-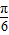 ≤2kπ+
≤2kπ+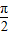 ,k∈z,求得 kπ-
,k∈z,求得 kπ-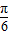 ≤x≤kπ+
≤x≤kπ+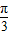 ,k∈z.
,k∈z. ,可得函数的增区间为[0,
,可得函数的增区间为[0,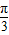 ]
]

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
| 3 |
|
|
查看答案和解析>>
科目:高中数学 来源:道里区三模 题型:单选题
| 1 |
| 2 |
| ||
| 2 |
A.-
| B.
| C.-
| D.
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省石家庄市精英中学高三(上)第一次调研数学试卷(文科)(解析版) 题型:选择题
 ),且2α∈[0,2π),则tanα等于( )
),且2α∈[0,2π),则tanα等于( )



查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省石家庄市精英中学高三(上)第一次调研数学试卷(文科)(解析版) 题型:选择题
 ),且2α∈[0,2π),则tanα等于( )
),且2α∈[0,2π),则tanα等于( )
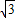
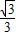

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com