设an是 的展开式中x的系数,则
的展开式中x的系数,则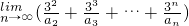 =________.
=________.
18
分析:先求出a
n =C
n2 3
n-2,化简
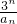
=18(
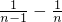
),代入要求的式子化简运算求得结果.
解答:二项式

的展开式的通项公式
Tr+1 =
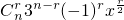
,
令r=2 可得x的系数 a
n =C
n2 3
n-2,∴
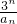
=
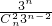
=
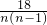
=18(
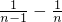
).
∴
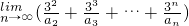
=
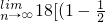
)+(

)+…+
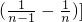
=

18(1-

)=18,
故答案为:18.
点评:本题主要考查二项展开式的通项公式,求展开式中某项的系数,用裂项法进行数列求和,求数列的极限,求出
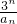
=
18(
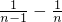
),是解题的关键.
练习册系列答案
相关习题
科目:高中数学
来源:2013年全国高校自主招生数学模拟试卷(九)(解析版)
题型:填空题
设a
n是
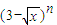
的展开式中x项的系数(n=2、3、4、…),则
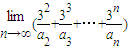
=
.
查看答案和解析>>
科目:高中数学
来源:2008-2009学年湖北省“鄂南高中、黄冈中学、黄石二中、华师一附中、荆州中学、襄樊四中、襄樊五中、孝感高中”八校高三第二次联考数学试卷(理科)(解析版)
题型:解答题
设a
n是
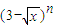
的展开式中x项的系数(n=2、3、4、…),则
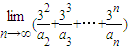
=
.
查看答案和解析>>
科目:高中数学
来源:2010年河南省豫南九校高考数学仿真模拟试卷(理科)(解析版)
题型:解答题
设a
n是
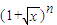
的展开式中x项的系数(n=2,3,4,…),则
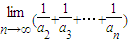
=
.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年重庆市南开中学高三(下)5月月考数学试卷(理科)(解析版)
题型:解答题
设a
n是
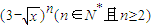
的展开式中x的系数,则
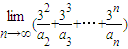
=
.
查看答案和解析>>
科目:高中数学
来源:2010年上海市奉贤区高考数学一模试卷(理科)(解析版)
题型:解答题
设a
n是
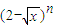
的展开式中x项的系数(n=2,3,4,…),则极限

=
.
查看答案和解析>>

 的展开式中x的系数,则
的展开式中x的系数,则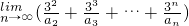 =________.
=________.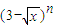 的展开式中x项的系数(n=2、3、4、…),则
的展开式中x项的系数(n=2、3、4、…),则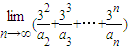 = .
= .