
【题目】已知函数![]() .
.
(1)若![]() 恒成立,求a的值;
恒成立,求a的值;
(2)在(1)的条件下,若![]() ,证明:
,证明:![]() ;
;
(3)若![]() ,证明:
,证明:![]() .
.
【答案】(1)1;(2)证明见解析;(3)证明见解析.
【解析】
(1)利用导数求函数的最小值,令最小值大于等于0,从而求得![]() 的值;
的值;
(2)由(1)可得![]() ,令
,令![]() ,利用导数求证函数的最小值大于等于0即可;
,利用导数求证函数的最小值大于等于0即可;
(3)由(2)可得,当![]() 时,
时,![]() ,要证
,要证![]() ,只需证明
,只需证明![]() ,若
,若![]() ,即
,即![]() ,再利用换元法,结合导数进行证明即可.
,再利用换元法,结合导数进行证明即可.
(1)由题可得![]() .
.
当![]() 时,若
时,若![]() ,则
,则![]() ,不满足条件.
,不满足条件.
当![]() 时,令
时,令![]() ,得
,得![]() .
.
∵当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() 的最小值为
的最小值为![]()
令![]() ,由题意可知
,由题意可知![]() .
.
令![]() ,得
,得![]() .
.
易知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
![]() .
.
再结合![]() 式得
式得![]() .
.
(2)由(1)可得![]() .
.
令![]() ,则
,则![]() .
.
令![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
![]()
![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
![]() .
.
(3)由(2)可得,当![]() 时,
时,![]() .
.
要证![]() ,只需证明
,只需证明![]() .
.
若![]() ,即
,即![]() ,则题中不等式成立,下面证明
,则题中不等式成立,下面证明![]() .
.
令![]() ,
,
求导得![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
![]() ,即
,即![]() ,
,
![]()


科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 的左、右顶点分别为
的左、右顶点分别为![]() 右焦点为
右焦点为![]() ,右准线l的方程为
,右准线l的方程为![]() ,过焦点F的直线与椭圆C相交于点A,B(不与点
,过焦点F的直线与椭圆C相交于点A,B(不与点![]() 重合).
重合).
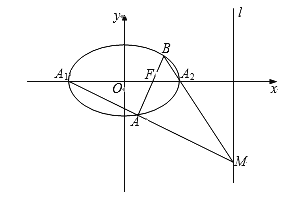
(1)求椭圆C的标准方程;
(2)当直线AB的倾斜角为45°时,求弦AB的长;
(3)设直线![]() 交l于点M,求证:B,
交l于点M,求证:B,![]() ,M三点共线.
,M三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省2020年高考将实施新的高考改革方案.考生的高考总成绩由3门统一高考科目成绩和自主选择的3门普通高中学业水平等级考试科目成绩组成,总分为750分.其中,统一高考科目为语文、数学、外语,自主选择的3门普通高中学业水平等级考试科目是从物理、化学、生物、政治、历史、地理6科中选择3门作为选考科目,语文、数学、外语三科各占150分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.根据高考综合改革方案,将每门等级考试科目中考生的原始成绩从高到低分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%.等级考试科目成绩计入考生总成绩时,将
共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%.等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则,分别转换到91~100,81~90,71~80,61~70,51~60,41~50,31~40,21~30八个分数区间,得到考生的等级成绩.举例说明:某同学化学学科原始分为65分,该学科
等级内的考生原始成绩,依照等比例转换法则,分别转换到91~100,81~90,71~80,61~70,51~60,41~50,31~40,21~30八个分数区间,得到考生的等级成绩.举例说明:某同学化学学科原始分为65分,该学科![]() 等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属
等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属![]() 等级.而
等级.而![]() 等级的转换分区间为61~70,那么该同学化学学科的转换分计算方法为:设该同学化学学科的转换等级分为
等级的转换分区间为61~70,那么该同学化学学科的转换分计算方法为:设该同学化学学科的转换等级分为![]() ,
,![]() ,求得
,求得![]() .四舍五入后该同学化学学科赋分成绩为67.为给高一学生合理选科提供依据,全省对六个选考科目进行测试,某校高一年级2000人,根据该校高一学生的物理原始成绩制成频率分布直方图(见右图).由频率分布直方图,可以认为该校高一学生的物理原始成绩
.四舍五入后该同学化学学科赋分成绩为67.为给高一学生合理选科提供依据,全省对六个选考科目进行测试,某校高一年级2000人,根据该校高一学生的物理原始成绩制成频率分布直方图(见右图).由频率分布直方图,可以认为该校高一学生的物理原始成绩![]() 服从正态分布
服从正态分布![]() ,用这2000名学生的平均物理成绩
,用这2000名学生的平均物理成绩![]() 作为
作为![]() 的估计值,用这2000名学生的物理成绩的方差
的估计值,用这2000名学生的物理成绩的方差![]() 作为
作为![]() 的估计值.
的估计值.
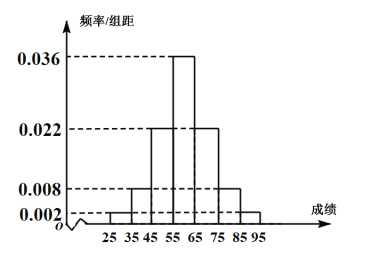
(1)若张明同学在这次考试中的物理原始分为86分,等级为![]() ,其所在原始分分布区间为82~93,求张明转换后的物理成绩(精确到1);按高考改革方案,若从全省考生中随机抽取100人,记
,其所在原始分分布区间为82~93,求张明转换后的物理成绩(精确到1);按高考改革方案,若从全省考生中随机抽取100人,记![]() 表示这100人中等级成绩在区间
表示这100人中等级成绩在区间![]() 内的人数,求
内的人数,求![]() 最有可能的取值(概率最大);
最有可能的取值(概率最大);
(2)①求![]() ,
,![]() (同一组中的数据用该组区间的中点作代表);
(同一组中的数据用该组区间的中点作代表);
②由①中的数据,记该校高一学生的物理原始分高于84分的人数为![]() ,求
,求![]() .
.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们知道,目前最常见的骰子是六面骰,它是一颗正立方体,上面分别有一到六个洞(或数字),其相对两面之数字和必为七.显然,掷一次六面骰,只能产生六个数之一(正上面).现欲要求你设计一个“十进制骰”,使其掷一次能产生0~9这十个数之一,而且每个数字产生的可能性一样.请问:你能设计出这样的骰子吗?若能,请写出你的设计方案;若不能,写出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD的三视图如下图所示,E是侧棱PC上的动点.
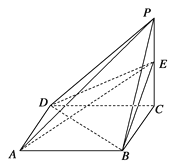

(1)求证:BD⊥AE
(2)若点E为PC的中点,求二面角D-AE-B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.![]() 是抛物线
是抛物线![]() 的焦点,过焦点的直线
的焦点,过焦点的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求抛物线![]() 的方程.
的方程.
(2)过点![]() ,
,![]() 作抛物线
作抛物线![]() 的切线
的切线![]() ,
,![]() ,
,![]() 是
是![]() ,
,![]() 的交点,求证:点
的交点,求证:点![]() 在定直线上.
在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是等边三角形,
的底面是等边三角形,![]() 在底面ABC上的射影为△ABC的重心G.
在底面ABC上的射影为△ABC的重心G.
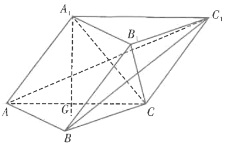
(1)已知![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
(2)已知平面![]() 与平面ABC所成的二面角为60°,G到直线AB的距离为a,求锐二面角
与平面ABC所成的二面角为60°,G到直线AB的距离为a,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com