
���� ���������������ֱ�ٳ�������˵���ٺ͢ڶ��Ǵ���ģ�ͬʱ֤���ۺ͢�����ȷ�ģ�
��� �⣺�ڢ��У�������f��x��=$\left\{\begin{array}{l}\frac{1}{{2}^{x}}��1��x��3\\ 2��x=3\end{array}\right.$��[1��3]����������P��
��f��x����[1��3]�ϲ��������������ʢٲ�������
�ڢ��У�������f��x��=-x��[1��3]����������P����f��x2��=-x2��[1��$\sqrt{3}$]�ϲ���������P��
�ʢڲ�������
�ڢ��У���[1��3]�ϣ�f��2��=f��$\frac{x+4-x}{2}$����$\frac{1}{2}$[f��x��+f��4-x��]��
��$\left\{\begin{array}{l}f��x��+f��4-x����2\\{f��x����f��x��}_{max}=f��2��=1\\{f��4-x����f��x��}_{max}=f��2��=1\end{array}\right.$��
��f��x��=1��
��������x1��x2��[1��3]��f��x��=1��
�ʢ۳�����
�ڢ��У�������x1��x2��x3��x4��[1��3]��
��f��$\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}}{4}$��=f��$\frac{{\frac{1}{2}��x}_{1}+{x}_{2}��+{\frac{1}{2}��x}_{3}+{x}_{4}��}{2}$��
��$\frac{1}{2}$[f��$\frac{{x}_{1}+{x}_{2}}{2}$��+f��$\frac{{x}_{3}+{x}_{4}}{2}$ ��]
��[$\frac{1}{2}$��f��x1��+f��x2����+$\frac{1}{2}$��f��x3��+f��x4����]
=$\frac{1}{4}$[f��x1��+f��x2��+f��x3��+f��x4��]��
��f��$\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}}{4}$����$\frac{1}{4}$[f��x1��+f��x2��+f��x3��+f��x4��]��
�ʢܳ�����
�ʴ�Ϊ���ۢܣ�
���� ���⿼���֪ʶ��Ϊ������������⣬˵��һ�����۴���ʱ��ֻ��ٳ��������ɣ�˵��һ��������ȷʱ��Ҫ֤�������е������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{2}}{2}$ | B�� | 1 | C�� | $\sqrt{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
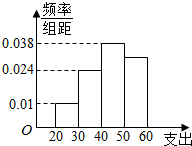 ѧУΪ�˵���ѧ���ڿ�����﷽���֧������������һ������Ϊn��֧����[20��60��Ԫ����������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������֧����[50��60��Ԫ��ѧ����30�ˣ���n��ֵΪ��������
ѧУΪ�˵���ѧ���ڿ�����﷽���֧������������һ������Ϊn��֧����[20��60��Ԫ����������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������֧����[50��60��Ԫ��ѧ����30�ˣ���n��ֵΪ��������| A�� | 100 | B�� | 1000 | C�� | 90 | D�� | 900 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5��}{4}$ | B�� | $\frac{2��}{5}$ | C�� | $��6-2\sqrt{5}����$ | D�� | $\frac{5��}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ1��1�� | B�� | ��һ2��2�� | C�� | ��һ1��2�� | D�� | ��һ2��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com