球的内接正方体的棱长为a,则该正方体同一棱的两端点间的球面距离均为 .
【答案】
分析:由已知中棱长为a的正方体ABCD-A
1B
1C
1D
1 的八个顶点都在球O的表面上,我们可以求出球O的半径,进而根据AA
1,解三角形AOA
1,求出∠AOA
1的大小,进而根据弧长公式,即可求出答案.
解答:解:设棱长为a的正方体ABCD-A
1B
1C
1D
1 的八个顶点都在球O的表面上,
故球O的直径等于正方体的对角线长
即2R=

a
∴R=
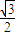
a
又∵AA
1=a,根据余弦定理得cos∠AOA
1=
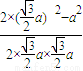
=

,
∴∠AOA
1=
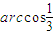
,
则A,A
1两点之间的球面距离为

.
故答案为:

.
点评:本题考查的知识点是球内接多面体,球面距离,其中根据已知条件求出球的关径,及弧AA
1对应的圆心角的度数是解答本题的关键.
