
已知数列{an},其中a2=6且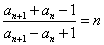 .
.
(1)计算a1,a3,a4;并求数列{an}的通项公式;
(2)设数列{bn}为等差数列,其中bn=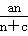
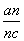 且c为不等于零的常数,求Sn=b1+b2+…+bn
且c为不等于零的常数,求Sn=b1+b2+…+bn
解:(1)∵a2=6, =1,
=1,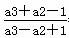 =2,
=2,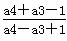 =3,解得a1=1,a3=15,a4=28.
=3,解得a1=1,a3=15,a4=28.
由上面的a1,a2,a3,a4的值可以猜想an=n(2n-1).
下面用数学归纳法加以证明:
①当n=1时,a1=1×(2-1)=1,结论成立.
②假设当n=k时,结论正确,即
ak=k(2k-1),
则当n=k+1时,有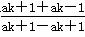 =k,
=k,
∴(k-1)ak+1=(k+1)ak-(k+1)=(k+1)·k(2k-1)-(k+1)=(k+1)(2k2-k-1)
=(k+1)(2k+1)(k-1)(k-1≠0).
∴ak+1=(k+1)[2(k+1)-1].
即当n=k+1时,结论也成立.由①②可知,{an}的通项公式
an=n(2n-1).
(2)∵{bn}是等差数列,∴2b2=b1+b3,即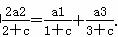
∵a1=1,a2=6,a3=15且c≠0,
由上式解得c=-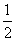 ∴bn=
∴bn=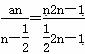 =2n.故Sn=b1+b2+…+bn=n(n+1).
=2n.故Sn=b1+b2+…+bn=n(n+1).


科目:高中数学 来源: 题型:
二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2,观察发现S′=l;三维空间中球的二维测度(表面积)S=4πr2,三维测度(体积)V=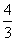 πr3,观察发现V′=S.则四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=_______.
πr3,观察发现V′=S.则四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-3)=0,则不等式f(x)g(x)<0的解集是( A )
A.(-∞,-3)∪(0,3) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞) D.(-3,0)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
设有一组圆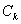 :
: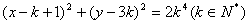 . 下列四个命题:
. 下列四个命题:
①存在一条定直线与所有的圆均相切; ②存在一条定直线与所有的圆均相交;
③存在一条定直线与所有的圆均不相交; ④所有的圆均不经过原点.
其中真命题的个数为
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com