练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    判断正误，并简要说明理由．

    ①a·0＝0；②0·a＝0；③0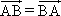－；④|a·b|＝|a||b|；⑤若a≠0，则对任一非零向量b有a·b≠0；⑥a·b＝0，则a与b中至少有一个为0；⑦a与b是两个单位向量，则a2＝b2．

    答案：
    解析：

    　　解：上述7个命题中只有③⑦正确：

    　　对于①：两个向量的数量积是一个实数，应有0·a＝0；

    　　对于②：应有0·a＝0；

    　　对于④：由数量积定义有|a·b|＝|a||b|·|cos|≤|a||b|，这里是a与b的夹角，只有＝0或＝π时，才有|a·b|＝|a||b|；

    　　对于⑤：若非零向量a、b垂直，则有a·b＝0；

    　　对于⑥：由a·b＝0可知a⊥b，可以都非零．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习高手必修四数学苏教版 苏教版 题型：044

    判断正误，并简要说明理由．

    ①a·0＝0；②0·a＝0；③0－＝；④|a·b|＝|a||b|；⑤若a≠0，则对任一非零b有a·b≠0；⑥a·b＝0，则a与b中至少有一个为0；⑦对任意向量a，b，c都有(a·b)c＝a(b·c)；⑧a与b是两个单位向量，则a2＝b2．

    查看答案和解析>>

    科目：高中数学 来源：101网校同步练习　高一数学　苏教版(新课标·2004年初审) 苏教版 题型：044

    判断正误，并简要说明理由．

    ①·＝；②0·＝0；③－＝；④|·|＝||||；⑤若≠，则对任一非零有·≠0；⑥·＝0，则与中至少有一个为；⑦对任意向量，，都有(·)＝(·)；⑧与是两个单位向量，则2＝2．

    评述：这一类型题，要求学生确实把握好数量积的定义、性质、运算律．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    判断正误，并简要说明理由.

    ①a·0=0；②0·a=0；③0-=；④|a·b|=|a||b|；⑤若a≠0，则对任一非零向量b有a·b≠0；⑥a·b=0，则a与b中至少有一个为0；⑦a与b是两个单位向量，则a2=b2.

    查看答案和解析>>

    同步练习册答案