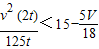据实验测出:汽车从刹车到停车所滑行的距离(m)与时速(km/h)的平方乘汽车总质量的积成正比例关系,设某辆卡车不装货物,以速度50km/h的速度行驶时,从刹车到停车走了20m,若这辆卡车装着同车等质量的货物行驶时,发现前方20m处有障碍物,为了能在离障碍物5m以外停车,最大限制时速应是多少(答案只保留整数,设卡车司机从发现障碍物到刹车需经过1s)
【答案】
分析:设从刹车到停车滑行的距离为S(m),时速为V(km/h),卡车总质量为t,比例常数为k,然后根据条件求出k的值,再根据滑行距离<到障碍物距离建立不等关系,解之即可求出所求,立式时注意单位的统一.
解答:解:设从刹车到停车滑行的距离为S(m),时速为V(km/h),卡车总质量为t,比例常数为k,
根据题意可得S=kv
2t
设卡车空载时的总质量为t
,则20=2500kt
,化简得k=
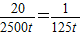
,故S=
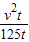
,
当卡车载物行驶时,t=2t
,1s=
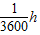
,1km=1000m
由滑行距离<到障碍物距离,得S<20-5-
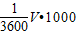
,即
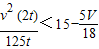
∴36V
2+625V-33750<0
解得0<V<23.14(四舍五入到百分位),取整数部分,最大限制时速为23km/h
答:最大限制速度为23km/h.
点评:本题主要考查了函数模型的选择与应用,以及一元二次不等式的应用,属于中档题.

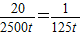 ,故S=
,故S=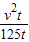 ,
,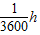 ,1km=1000m
,1km=1000m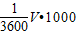 ,即
,即