练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    经过圆x2+y2+2y=0的圆心C，且与直线2x+3y-4=0平行的直线方程为（ ）
    A．2x+3y+3=0
    B．2x+3y-3=0
    C．2x+3y+2=0
    D．3x-2y-2=0
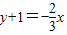
    【答案】分析：由圆x2+y2+2y=0得x2+（y+1）2=1，圆心坐标为C（0，-1），利用点斜式可得：经过圆心C，且与直线2x+3y-4=0平行的直线方程为，即可．
    解答：解：由圆x2+y2+2y=0得x2+（y+1）2=1，圆心坐标为C（0，-1），直线2x+3y-4=0的斜率，
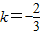
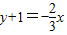
    ∴经过圆心C，且与直线2x+3y-4=0平行的直线方程为，即2x+3y+3=0．
    故选A．
    点评：熟练掌握圆的标准方程、相互平行的直线的斜率之间的关系、点斜式是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若直线ax-by+1=0（a＞0，b＞0）经过圆x2+y2+2x-2y=2的圆心，则
    1
    a
    +
    1
    b
    的最小值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    经过点（1，1）且与圆x2+y2=2相切的直线的方程是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若直线ax-by+2=0（a＞0，b＞0）经过圆x2+y2+2x-2y=7的圆心，则ab的最大值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    圆x2+y2=2的经过点P（
    		2
    ，2-
    		2
    ）的切线方程是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线ax+by+c-1=0（b、c＞0）经过圆x2+y2-2y-5=0的圆心，则
    4
    b
    +
    1
    c
    的最小值是（　　）
    A、9B、8C、4D、2

    查看答案和解析>>

    同步练习册答案